第 3 章优化算法

3.1 介绍

优化算法的历史由来已久。牛顿（Newton）和和高斯（Gauss）提出了迭代方法以求出最佳值。十九世纪的法国大数学学皮埃尔·德·费马(Pierre de Fermat)和约瑟夫·拉格朗日伯爵(Lagrange)找到了基于代数公式来确定佳值的方法。

优化算法中著名的“线性编程”（linear programming）一词是由George B. Dantzig提出的，该理论的许多内容是由Leonid Kantorovich于1939年提出的。这里特别要指出的是在这种情况下，编程不是指计算机编程，而是是指用于美国军方的优化训练和后勤保障时间的一种方法。该方法当时由Dantzig提出。 Dantzig在1947年发表了著名的单纯型算法，而计算机学家冯诺依曼（John von Neumann）在同年提出了对偶理论。

现代优化算法发展大概经历了三个阶段的发展。

第一代的优化方法的大多数考虑局部最优，即最低点或最低点。全局最优值定义为所有谷值的最低点，这超出了这些方法的能力。

有些算法涉及到迭代搜索。迭代搜索的思想是基于先前探索点的位置。它的比喻就像一个盲人爬山。此人必须知道他们的当前位置，移动方向和移动距离才能确定下一个位置。搜索过程会反复进行，直到到达山顶为止。当每个步骤花费很长时间时，此方法会遇到困难，因为优化的总时间等于每个步骤经过的时间与所采取步骤的数量的乘积。

还有些算法对梯度或更高阶导数的依赖很强。梯度甚至更高阶导数的计算需要更多的计算资源，并且比其他方法更容易出错。现代计算机的自动微分工具很大程度上解决了这一问题。在应用中，这些方法无法解释为什么最优是最优的。另外，由于计算能力有限，这些方法并未在工程中得到广泛应用。一些商业软件工具或者开源软件如R，CPLEX，LINDO，GAMS，SNOPT和MATLAB均部署了这些算法。

第二代优化算法出现在1980年代。工程师中使用最流行的方法之一是遗传算法（Genetic Algorithms），该算法由约翰·霍兰德（John Holland）于1960年发明。遗传算法的工作原理是“适者生存”。之后，模拟退火算法（Simulated Annealing）于1983年发表在《科学》杂志上。早期的科学杂志很少刊登具体的算法，该算法文章出现在该期刊是极不寻常的。模拟退火算法是一种全局优化算法，其灵感来自退火的物理热处理过程。

后来开发了更多算法，例如粒子群优化，蚁群优化，禁忌搜索和人工蜂群。这组方法受自然界或其他启发式方法的启发。这些算法本质上是全局优化方法，而且它们不需要梯度的计算或更高的导数，他们也自然的支持并行计算。尽管这类算法有很多好处，但是主要问题是在达到全局最优值之前需要大量的试验点。这些方法非常适合仅由方程式组成的问题，或者仅需很少计算即可评估每个试验的效果。但是，在工程中，由于计算机辅助工程（CAE）工具被广泛采用和应用，评估每个设计的计算时间可能是数小时或数天。即使使用并行计算，评估数千个设计试验的总时间仍然是不切实际的。

基于AI的方法在1990年代后期开始出现，成为第三代优化方法，并在最近几年逐渐成熟。这一代算法的思路是使用有限数量的设计试验（称为样本点）在设计变量和目标/约束之间构建机器学习模型。可以根据传统的实验设计（DOE）生成采样点，

基于AI的方法的一大障碍是所谓的“维数诅咒”。由于需要一个样点来学习一个空间，假设每个维度仅使用三个点，对于一个10维问题，设计试验点的数量为59,049（即3 ^ 10）。设计试验次数的增长是指数级的，因此成为诅咒。由于这个原因，早期的基于AI的方法只能解决10维或更小的问题，并且很难解决高维问题。大量的机器学习和深度学习理论被应用到这里解决这一问题。

3.2 牛顿优化算法

假设函数 $f(x)$ 可导并一阶导 $f^{\prime}(x)$ 连续，那么最大化 $f(x)$ 相当于求 $f^{\prime}(x) = 0$ 的根，我们就可以使用牛顿法求根。优化 $f(x)$ 就转化成了方程求根问题。牛顿优化算法的迭代过程如下。

牛顿优化算法

选择初始猜测点 $x_0$，设置 $n = 0$。
按照以下迭代过程进行迭代：

\[x_{n+1}=x_{n}-\frac{f^{\prime}\left(x_{n}\right)}{f^{\prime\prime}\left(x_{n}\right)}.\]

计算 $|f^{\prime}(x_{n+1})|$。
1. 如果 $|f^{\prime}(x_{n+1})| \leq \epsilon$，停止迭代；
2. 否则，返回第 2 步。

上述优化过程的停止条件还可以为：

$|x_{n} - x_{n-1}| < \epsilon$.
$|f(x_{n}) - f(x_{n-1})| < \epsilon$.

3.3 多元优化算法

我们现在考虑多元优化算法，假设 $f: \mathbb{R}^d \rightarrow \mathbb{R}$，且 $f$ 的一阶和二阶偏导连续可导。我们记 $\mathbf{x} = (x_1, x_2, \cdots, x_d)^T$，那么我们有梯度向量

\[\nabla f(\mathbf x) = \frac{\partial f({\mathbf{x}})}{\partial {\mathbf{x}}} = \left( \begin{array}{c} \frac{\partial f(\mathbf x)}{\partial x_1}\\ \frac{\partial f(\mathbf x)}{\partial x_2}\\ \vdots\\ \frac{\partial f(\mathbf x)}{\partial x_d} \end{array} \right)\] 以及海塞矩阵

\[\mathbf{H}(\mathbf x)= \frac{\partial^2 f({ \mathbf{x}})}{\partial {\mathbf{x}}\partial{\mathbf{x}}'}= \left(\begin{array}{cccc}\frac{\partial^{2} f(\mathbf x)}{\partial x_{1}^{2}} & \frac{\partial^{2} f(\mathbf x)}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f(\mathbf x)}{\partial x_{1} \partial x_{d}} \\ \frac{\partial^{2} f(\mathbf x)}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f(\mathbf x)}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f(\mathbf x)}{\partial x_{2} \partial x_{d}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f(\mathbf x)}{\partial x_{d} \partial x_{1}} & \frac{\partial^{2} f(\mathbf x)}{\partial x_{d} \partial x_{2}} & \cdots & \frac{\partial^{2} f(\mathbf x)}{\partial x_{d}^{2}}\end{array}\right).\] 和一元优化问题类似，我们可以通过迭代求 $f(\mathbf x)$ 的极值。比如多元的牛顿优化算法的迭代过程可以写为：

\[\mathbf{x_{n+1}}=\mathbf{x_n}-\left(\frac{\partial^2 f({ \mathbf{x}})}{\partial {\mathbf{x}}\partial{\mathbf{x}}'}\right)^{-1}\frac{\partial f({\mathbf{x}})}{\partial {\mathbf{x}}}.\] 停止条件可以为：

$||\nabla f(\mathbf x_n)|| < \epsilon$.
$||\mathbf x_n - \mathbf x_{n-1}|| < \epsilon$.
$|f(\mathbf x_n) - f(\mathbf x_{n-1})|| < \epsilon$.

例3.1 通过牛顿优化算法求 $f(x_1, x_2) = x_1^2 - x_1x_2 + x_2^2 + \exp(x_2)$ 的最小值。

newton <- function(f, x0, tol = 1e-9, max.iter = 100) {
  x <- x0
  cat(paste0('初始值：','x1 = ',x[1],', x2 = ',x[2],'\n'))
  fx <- ftn(f, x)
  iter <- 0
  # xs用来保存每步迭代得到的x值
  xs <- list()
  xs[[1]] <- x
  # 继续迭代直到满足停止条件
  while((max(abs(fx$fgrad)) > tol) & (iter < max.iter)){
    x <- x - solve(fx$fhess, fx$fgrad)
    fx <- ftn(f, x)
    iter <- iter + 1
    xs[[iter + 1]] <- x
    cat(paste0('迭代第', iter, '次：x1 = ', x[1], ', x2 = ',
               x[2], '\n'))
  }
  if (max(abs(fx$fgrad)) > tol){
    cat('算法无法收敛 \n')
  } else{
    cat('算法收敛\n')
    return(xs)
  }
}

ftn <- function(f, x){
  df <- deriv(body(f), c('x1', 'x2'), func = TRUE,
              hessian = TRUE)
  dfx <- df(x[1], x[2])
  f <- dfx[1]
  fgrad <- attr(dfx, 'gradient')[1,]
  fhess <- attr(dfx, 'hessian')[1,,]
  return(list(f = f, fgrad = fgrad, fhess = fhess))
}
f <- function(x1, x2) x1^2 - x1 * x2 + x2^2 + exp(x2)

#> 初始值：x1 = 5, x2 = 5
#> 迭代第1次：x1 = 1.97998841450638, x2 = 3.95997682901276
#> 迭代第2次：x1 = 1.4388441844607, x2 = 2.8776883689214
#> 迭代第3次：x1 = 0.865775331919303, x2 = 1.73155066383861
#> 迭代第4次：x1 = 0.289032888354303, x2 = 0.578065776708607
#> 迭代第5次：x1 = -0.114564289467867, x2 = -0.229128578935734
#> 迭代第6次：x1 = -0.212927882981344, x2 = -0.425855765962689
#> 迭代第7次：x1 = -0.21627797375019, x2 = -0.43255594750038
#> 迭代第8次：x1 = -0.216281377762501, x2 = -0.432562755525002
#> 算法收敛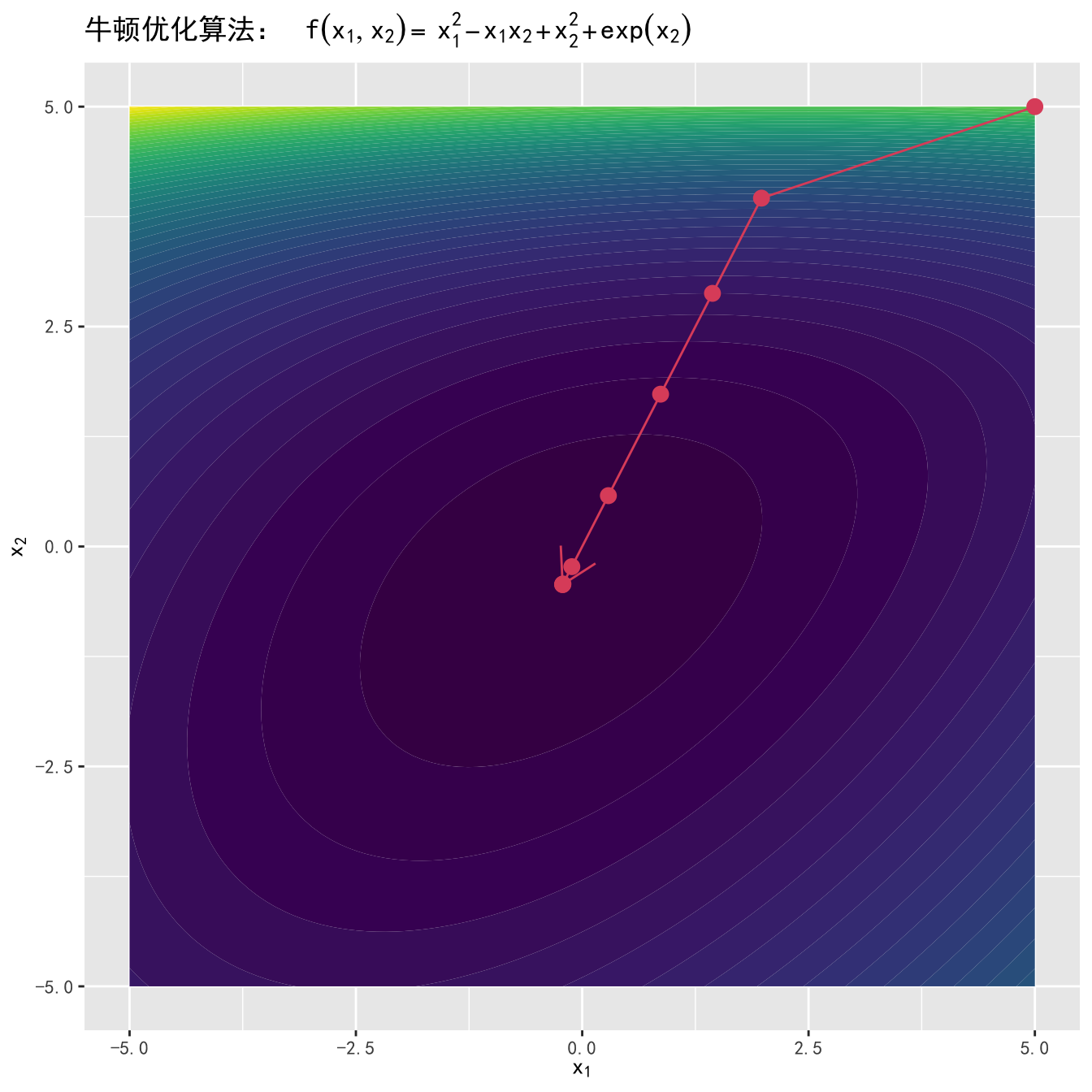

3.4 Nelder Mead 算法

在很多实际应用问题中，待优化的函数不可导，这就需要不依赖于求导的优化算法，Nelder Mead 算法，是最常用的不依赖于求导的算法之一，也是 R 中 optim() 函数的默认算法。

Nelder Mead 算法的思路是计算目标函数 $f(\cdot)$ 在 $n$ 维单纯形顶点出的取值，其中 $n$ 为 $f(\cdot)$ 中的变量个数，所以 Nelder Mead 算法有时也被称为单纯形优化法。对于一个二维函数，单纯形即为三角形，三角形的每一个角是一个顶点。更一般的，$n$ 维单纯形有 $n + 1$ 个顶点。

图 3.1 展示了一个二维单纯形的例子。

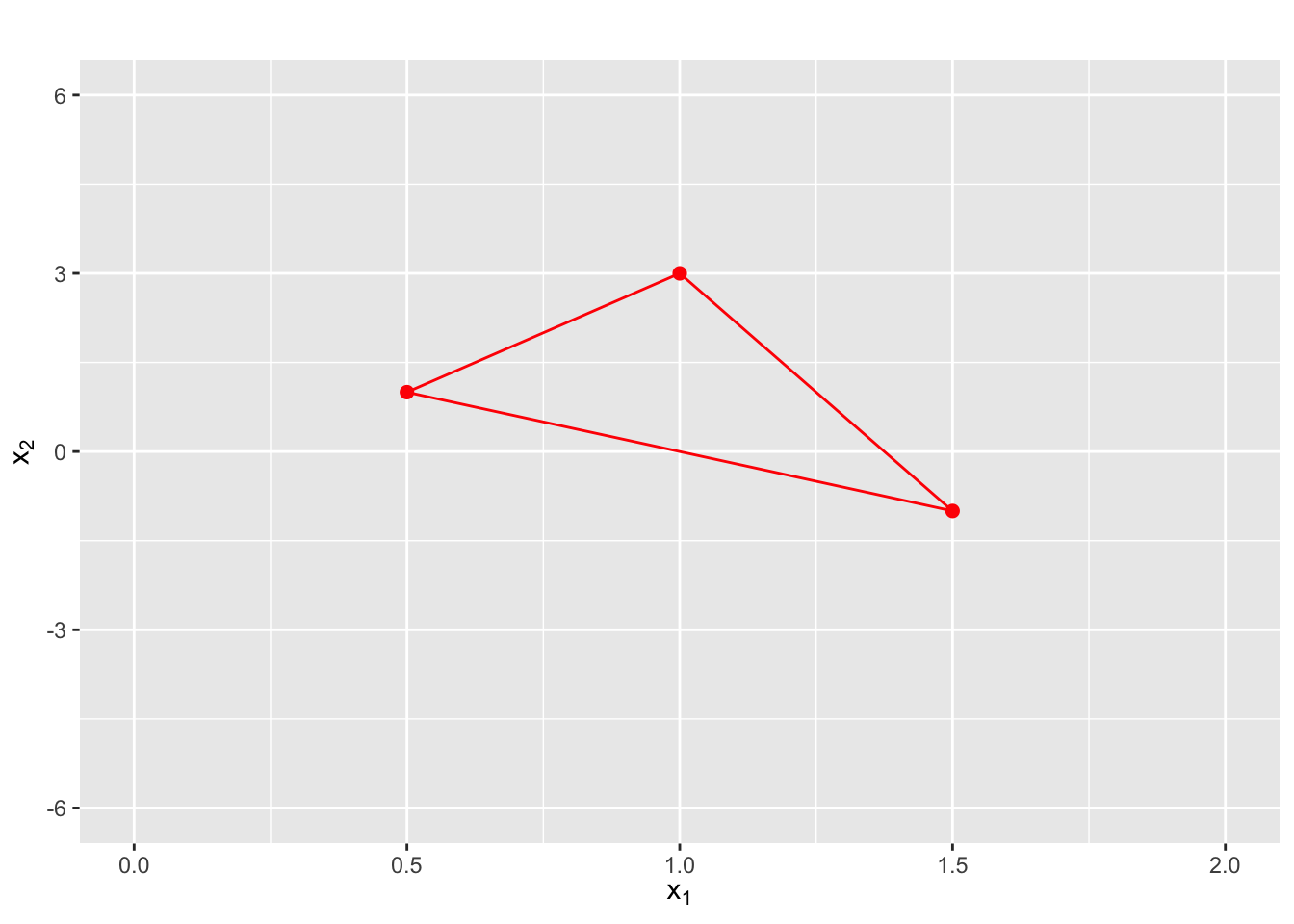
图3.1: 二维单纯形示例

第一步：求函数值

对每个单纯形的顶点 ${\mathbf x_j}$，计算函数值 $f({\mathbf x_j})$，其中 $j \in 1, 2, \cdots, n$，并将将所有顶点排序使得

\[f({\mathbf x_1})\leq f({\mathbf x_2})\leq\ldots\leq f({\mathbf x_{n+1}}).\] 假设我们的目标是最小化 $f(\cdot)$，那么 $f({\mathbf x_{n+1}})$ 就是最差点。算法目标即使寻找更好的点来取代 $f({\mathbf x_{n+1}})$。

第二步：计算中心点

去掉最差点 ${\mathbf x_{n+1}}$，计算剩下的 $n$ 个点的中心点，

\[{\mathbf x_0}=\frac{1}{n}\sum_{j=1}^{n} {\mathbf x_j}.\] 对于一个二维单纯形，中点即为两点连线的中点。

第三步：计算映射点

根据中点计算最差点的映射，得到映射点（Reflection Point）：

\[{\mathbf x_r}={\mathbf x_0}+\alpha({\mathbf x_0}-{\mathbf x_{n+1}}),\]

通常取 $\alpha=1$，这种情况下映射点和最差点到中点的距离相等。算法的下一步则取决于 $f({\mathbf x_r})$ 的取值大小。

$f({\mathbf x_1})\leq f({\mathbf x_r})<f({\mathbf x_n})$，这种情况下 ${\mathbf x_r}$ 既不是最佳点也不是最差点，将 $\mathbf x_{n+1}$ 替换为 ${\mathbf x_r}$，形成新的单纯形，回到第一步。
$f({\mathbf x_r})<f({\mathbf x_1})$，即 ${\mathbf x_r}$ 为最佳点，那么在这个方向上继续延伸，得到延伸点（Expansion Point）：

\[ {\mathbf x_e}={\mathbf x_0}+\gamma({\mathbf x_r}-{\mathbf x_0})，\] 通常取 $\gamma = 2$。计算 $f({\mathbf x_e})$。 - 如果 $f({\mathbf x_e}) < f({\mathbf x_r})$，那么延伸点比映射点更优，用延伸点 ${\mathbf x_e}$ 形成新的单纯形。 - 如果 $f({\mathbf x_r})\leq f({\mathbf x_e})$，用映射点 ${\mathbf x_r}$ 形成新的单纯形。

$f({\mathbf x_r})\geq f({\mathbf x_n})$，即 ${\mathbf x_r}$ 为最差点，这意味着在 ${\mathbf x_{n+1}}$ 和 ${\mathbf x_{r}}$ 之间可能存在谷点，这时寻找收缩点（contraction point）：

\[{\mathbf x_c}={\mathbf x_0}+\rho({\mathbf x_{n+1}}-{\mathbf x_0}),\] 通常取 $\rho=0.5$。 - 如果 $f({\mathbf x_c}) < f({\mathbf x_{n+1}})$，那么用收缩点 ${\mathbf x_c}$ 形成新的单纯形。 - 如果 $f({\mathbf x_c}) \geq f({\mathbf x_{n+1}})$，说明收缩无效，需要一个更小的单纯形，这时将 ${\mathbf x_{1}}$ 以外的点按以下方式压缩（shrink）：

\[{\mathbf x_i}={\mathbf x_1}+\sigma({\mathbf x_i}-{\mathbf x_1}),\] 通常取 $\sigma = 0.5$，得到新的单纯形后返回第一步。

由此可见，Nelder Mead 算法只用到了函数值，不依赖于求导函数，是一种比较稳健的优化算法。

图 3.2 展示了 Nelder Mead 算法优化函数 $f(x_1, x_2) = x_1^2 + x_2^2 + x_1\sin(x_2) + x_2\sin(x_1)$。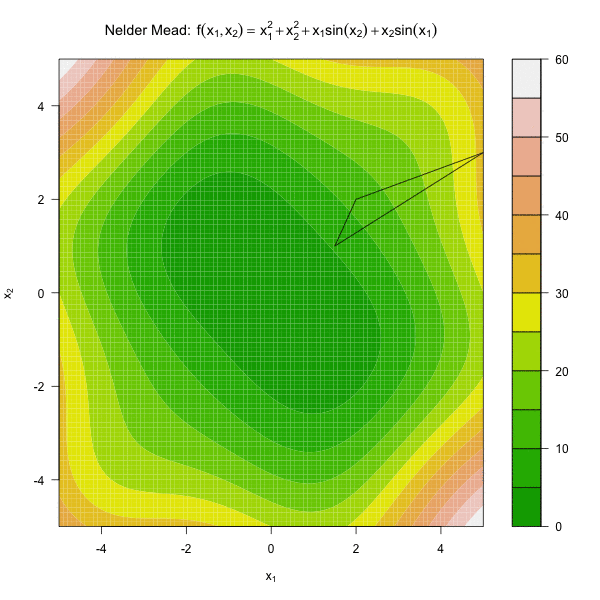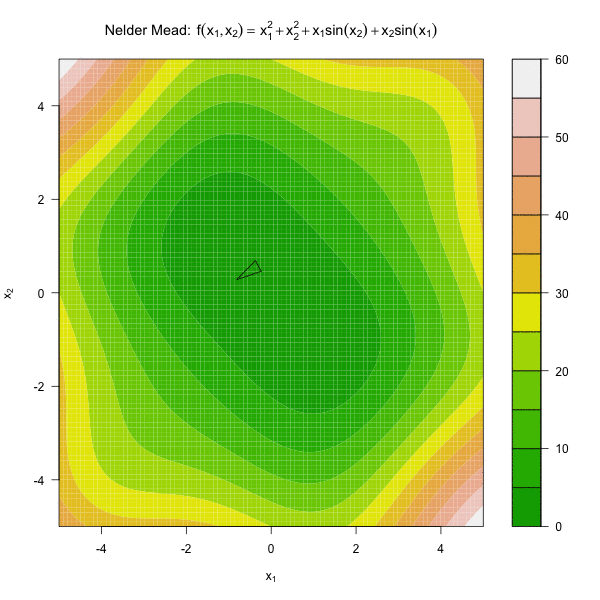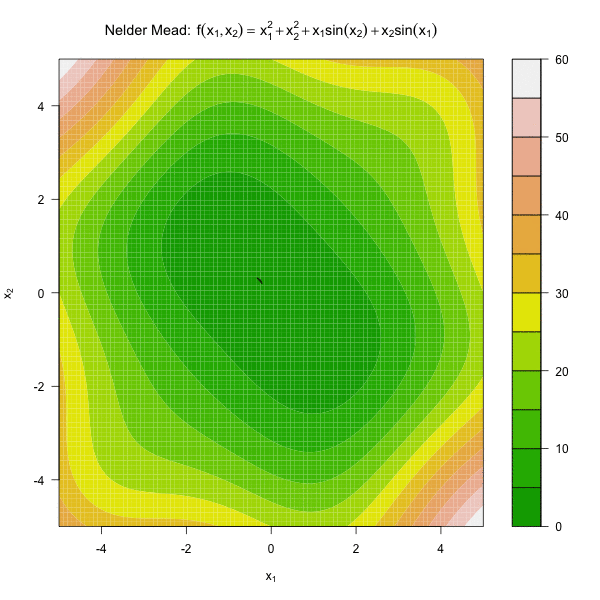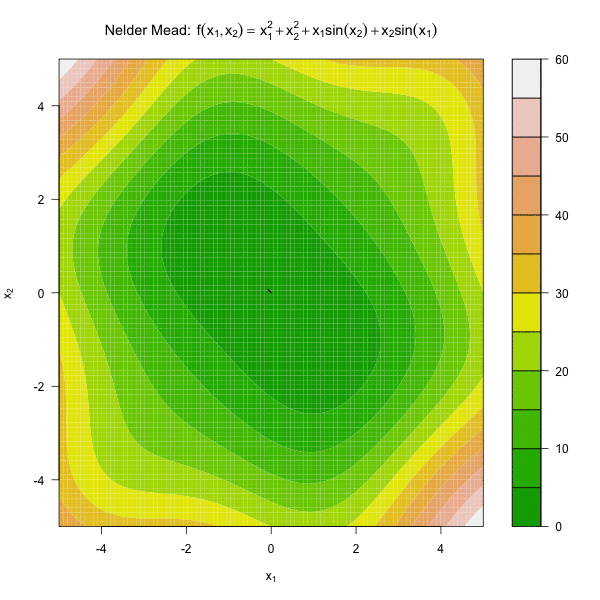

图3.2: 单纯形法优化动图

停止条件

由图 3.2 可见，随着迭代过程，单纯形的体积越来越小，因此通常将单纯形的体积足够小做为Nelder Mead。有 $n+1$ 个顶点的单纯形的体积为：

\[\frac{1}{2}|\mathrm{det}(\tilde{X})|,\] 其中

\[\tilde{X}=\left({\mathbf x_1}-{\mathbf x_{n+1}},{\mathbf x_2-{\mathbf x_{n+1}}},\ldots, {\mathbf x_{n}-{\mathbf x_{n+1}}}\right).\]

在 R 中，Nelder Mead 算法可以用 optim() 实现。

3.5 随机梯度下降算法

3.5.1 梯度下降算法

梯度下降（Gradient Descent，或者 Steepest Descent）算法是一种迭代算法。对于一个多元连续可导函数 $f(\mathbf{x})$，在 $\mathbf{x}_n$ 处 $f(\mathbf{x})$下降最快的方向也就是$f(\mathbf{x})$ 在 $\mathbf{x}_n$ 处的梯度方向的反方向，即$-\nabla f(\mathbf{x}_n)$，这也是与 $\mathbf{x}_n$ 处等高线正交的方向。所以给定当前 $\mathbf{x}_n$，梯度下降算法的更新策略就是：

\[\begin{equation} \mathbf{x}_{n+1}=\mathbf{x}_{n}-\alpha \nabla f\left(\mathbf{x}_{n}\right), \tag{3.1} \end{equation}\]

其中 $\alpha > 0$ 控制下降步长。我们可以选择 $\alpha$ 以最小化：

\[\begin{equation} g(\alpha) = f(\mathbf{x}_n - \alpha \nabla f(\mathbf{x}_n), \tag{3.2} \end{equation}\] 如果我们的初始猜测为 $\mathbf{x}_0$，那么根据公式 (3.1)，我们可以得到 $f(\mathbf{x}_0) \geq f(\mathbf{x}_1) \geq f(\mathbf{x}_2) \geq \cdots$，如果算法收敛，序列 $\{\mathbf{x}_n\}$ 就会收敛到 $f(\mathbf{x})$ 的局部极小值。所以我们可以以 $f(\mathbf{x}_{n+1})- f(\mathbf{x}_n) \leq \epsilon$ 为梯度下降算法收敛的停止条件，其中 $\epsilon$ 为容忍值。

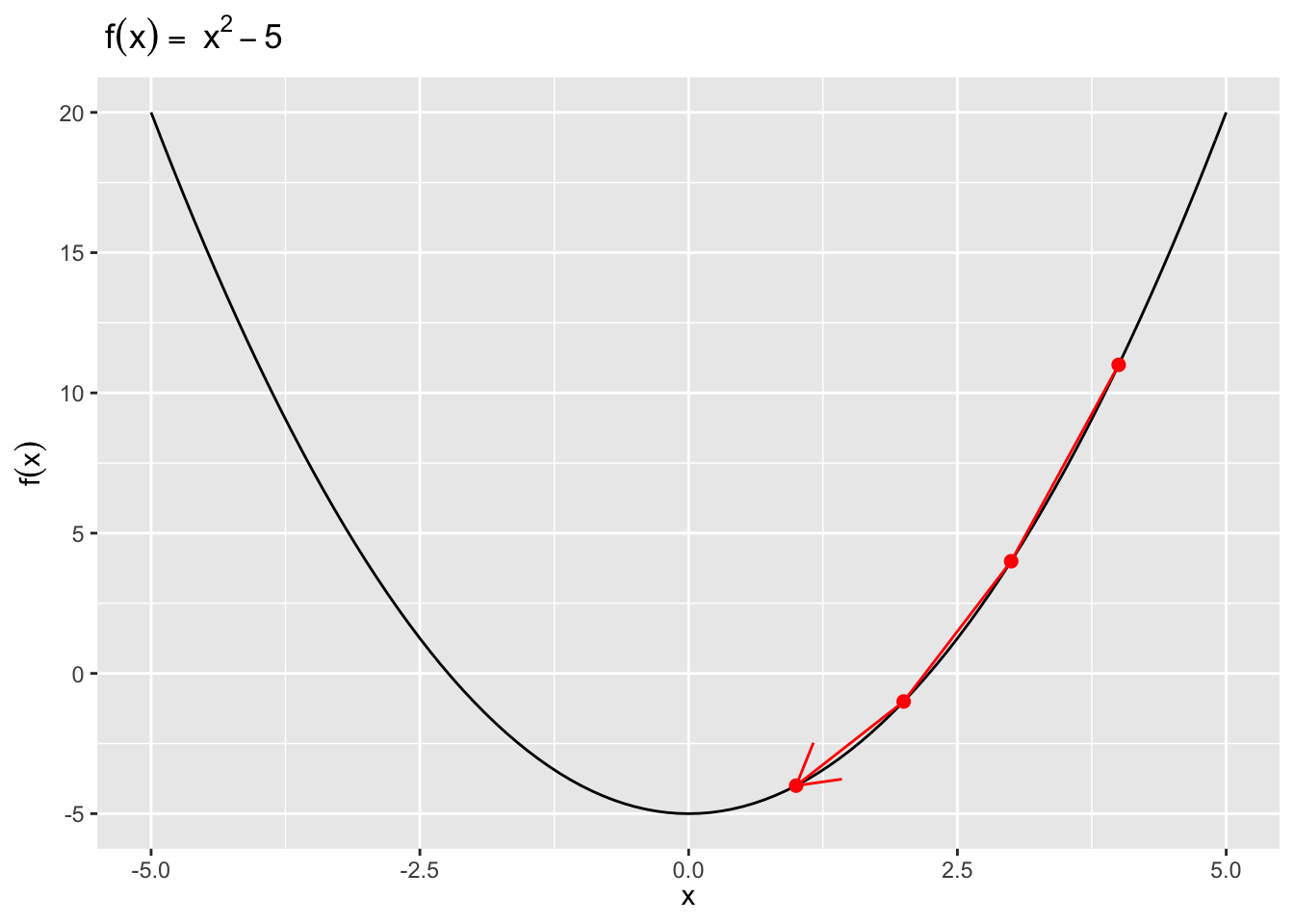
图3.3: 梯度下降算法：一元函数

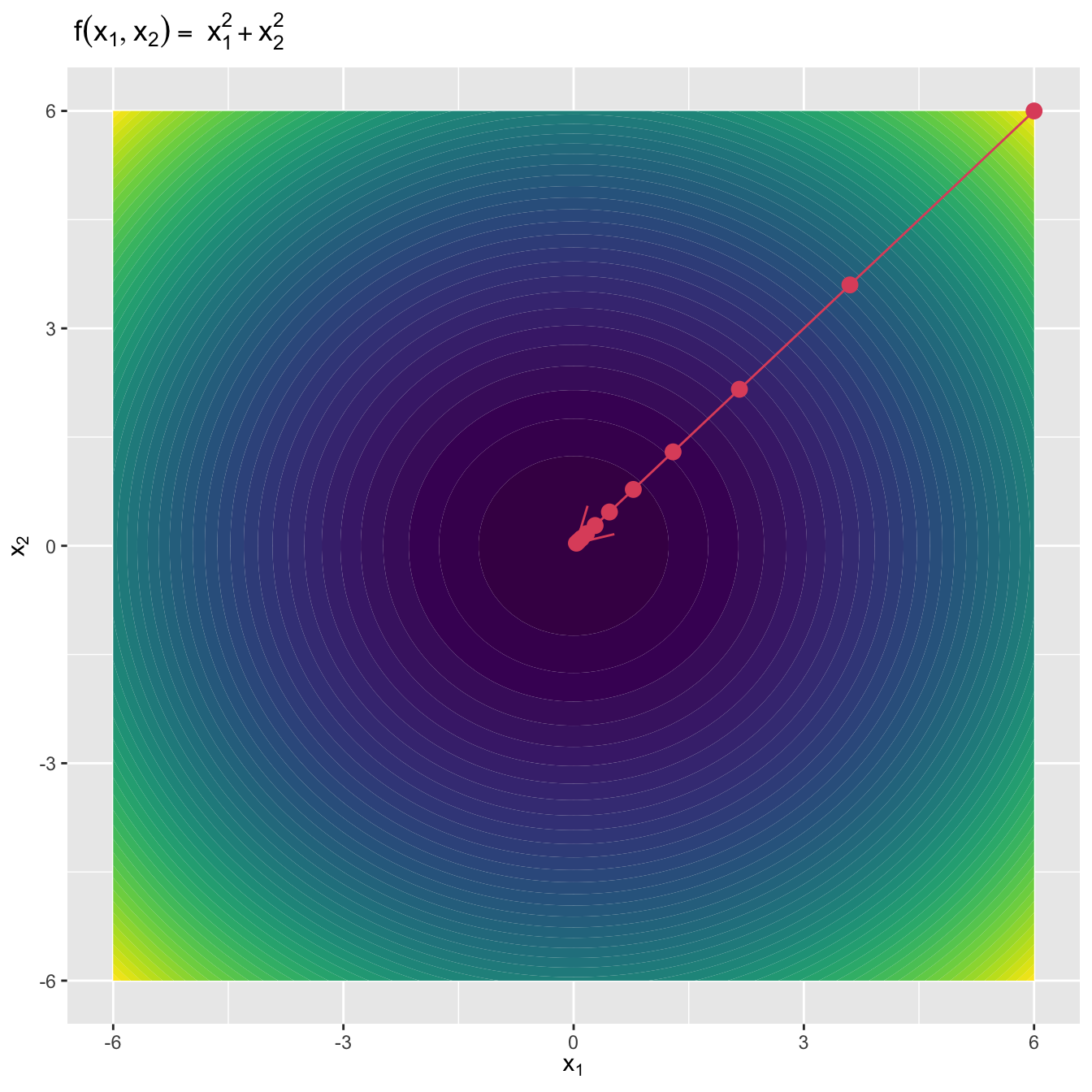
图3.4: 梯度下降算法：二元函数

值得注意的是，通常情况下梯度反方向迭代是符合逻辑的，但是当待优化函数中的某些参数存在高度相关关系时，梯度下降算法的收敛速度可能会降低。

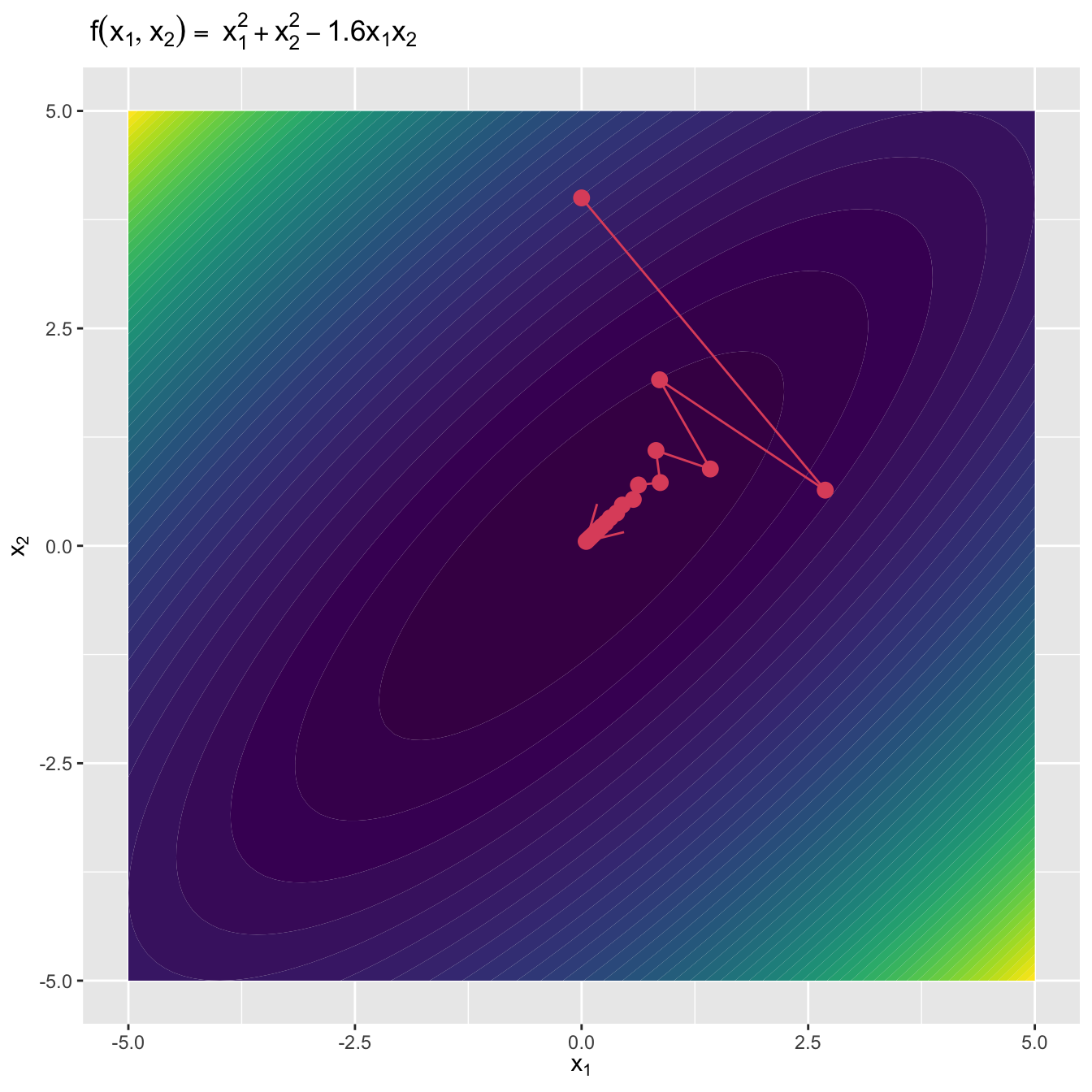
图3.5: 梯度下降算法（变量高度相关的情况）

例3.2 用梯度下降算法估计线性回归模型。

假设一般的线性回归模型 $y = X\beta + \eta,~\eta \sim N(0, I)$，给定 $n$ 个观测样本，我们可以写出线性模型的损失函数

\[J(\beta) = \frac{1}{2n}(X\beta - y)^T(X\beta - y).\] 对应的梯度向量为

\[\nabla J(\beta) = \frac{1}{n}X^T(X\beta-y).\]

gd.lm <- function(X, y, beta.init, alpha, tol = 1e-5,
                  max.iter = 100){
  beta.old <- beta.init
  J <- betas <- list()
  if (alpha == 'auto'){
    alpha <-
      optim(0.1, function(alpha) {
        lm.cost(
          X, y,
          beta.old - alpha * lm.cost.grad(X, y, beta.old))
      }, method = 'L-BFGS-B', lower = 0, upper = 1)
    if (alpha$convergence == 0) {
      alpha <- alpha$par
    } else{
      alpha <- 0.1
    }
  }
  betas[[1]] <- beta.old
  J[[1]] <- lm.cost(X, y, beta.old)
  beta.new <- beta.old -
    alpha * lm.cost.grad(X, y, beta.old)
  betas[[2]] <- beta.new
  J[[2]] <- lm.cost(X, y, beta.new)
  iter <- 0
  while ((abs(lm.cost(X, y, beta.new) -
              lm.cost(X, y, beta.old))  > tol) &
         (iter < max.iter)) {
    beta.old <- beta.new
    if (alpha == 'auto'){
    alpha <-
      optim(0.1, function(alpha) {
        lm.cost(X, y, beta.old -
          alpha * lm.cost.grad(X, y, beta.old))},
        method = 'L-BFGS-B', lower = 0, upper = 1)
    if (alpha$convergence == 0) {
      alpha <- alpha$par
    } else{
      alpha <- 0.1
    }
    }
    beta.new <- beta.old -
      alpha * lm.cost.grad(X, y, beta.old)
    iter <- iter + 1
    betas[[iter + 2]] <- beta.new
    J[[iter + 2]] <- lm.cost(X, y, beta.new)
  }
  if (abs(lm.cost(X, y, beta.new) -
          lm.cost(X, y, beta.old)) > tol){
    cat('算法无法收敛 \n')
  } else{
    cat('算法收敛\n')
    cat('共迭代',iter + 1,'次','\n')
    cat('系数估计为：', beta.new, '\n')
    return(list(coef = betas,
                cost = J,
                niter = iter + 1))
  }
}

## Generate some data
beta0 <- 1
beta1 <- 3
sigma <- 1
n <- 10000
x <- rnorm(n, 0, 1)
y <- beta0 + x * beta1 + rnorm(n, mean = 0, sd = sigma)
X <- cbind(1, x)

## Make the cost function
lm.cost <- function(X, y, beta){
   n <- length(y)
   loss <- sum((X%*%beta -  y)^2)/(2*n)
return(loss)
}
## Calculate the gradient
lm.cost.grad <- function(X, y, beta){
  n <- length(y)
  (1/n)*(t(X)%*%(X%*%beta - y))
}
## Use optimized alpha
gd.auto <- gd.lm(X, y, beta.init = c(-4,-5), alpha = 'auto',
                 tol = 1e-5, max.iter = 10000)
#> 算法收敛
#> 共迭代 3 次 
#> 系数估计为： 0.9939 3

## alpha = 0.1
gd1 <- gd.lm(X, y, beta.init = c(-4,-5), alpha = 0.1,
             tol = 1e-5, max.iter = 10000)
#> 算法收敛
#> 共迭代 67 次 
#> 系数估计为： 0.9896 2.993

## alpha = 0.01
gd2 <- gd.lm(X, y, beta.init = c(-4,-5), alpha = 0.01,
             tol = 1e-5, max.iter = 10000)
#> 算法收敛
#> 共迭代 570 次 
#> 系数估计为： 0.9778 2.973

niter <- data.frame(alpha = c('auto', 0.1, 0.01),
                    niter = c(gd.auto$niter, gd1$niter, 
                              gd2$niter))
knitr::kable(
  niter, caption = '不同 $\\alpha$ 对应的梯度下降算法的迭代次数',
  booktabs = TRUE,  col.names = c("$\\alpha$", '迭代次数'),

)

表3.1: 不同 $\alpha$ 对应的梯度下降算法的迭代次数
$\alpha$	迭代次数
auto	3
0.1	67
0.01	570

从表_3.1中我们可以发现在每次迭代过程中对 $\alpha$ 进行优化可以显著提高计算效率。如图_3.6，如果 $\alpha$ 较小，迭代的次数就会增加，因此收敛过程比较缓慢。

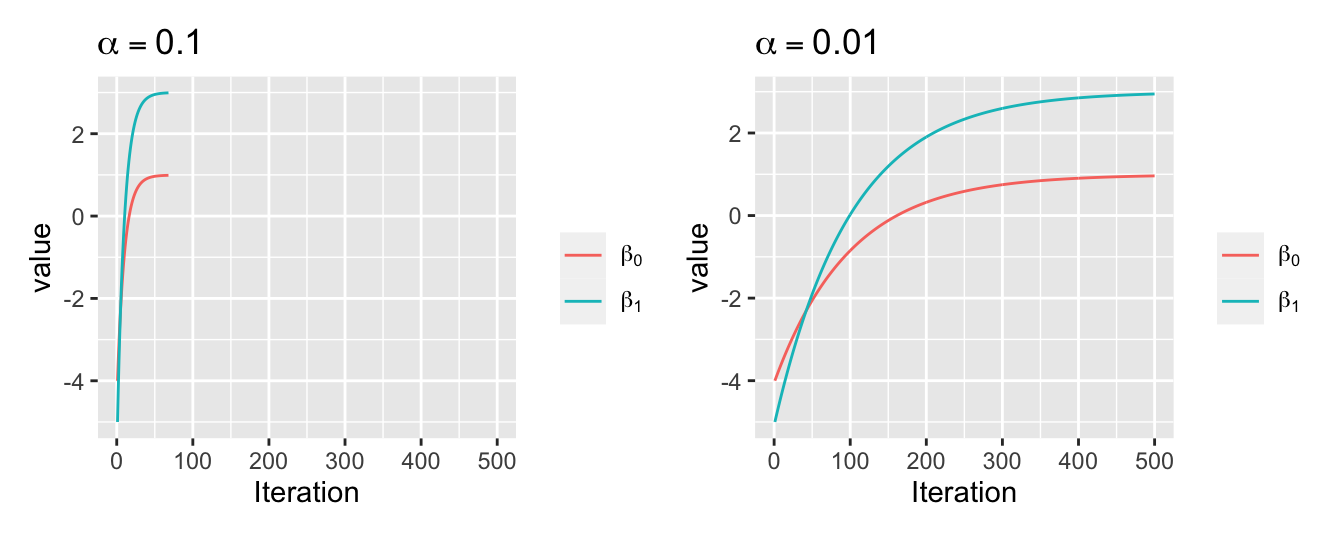
$不同 $\alpha$ 取值下梯度下降算法的收敛情况$

图3.6: 不同 $\alpha$ 取值下梯度下降算法的收敛情况

3.5.2 随机梯度下降算法

梯度下降算法通常收敛速度较慢，因为在每次迭代中对每个样本值都需要计算梯度，在样本量较大时计算量会随之增大。随机梯度下降算法的思想是在算法的每次迭代更新时只考虑一个样本。以线性回归模型为例，就是将梯度下降算法中的

\[\nabla J(\beta) = \frac{1}{n}X^T(X\beta-y).\] 替换为：

\[\nabla J(\beta)_i = X_i^T(X_i\beta-y_i),\] 完整的迭代过程如下。

随机梯度下降算法

将训练数据随机排序，然后重复第2步直至收敛。
抽取一个随机样本 $i\in\{1, 2, \cdots, n\}$，根据下式对 $\beta$ 进行迭代。

\[\beta:= \beta - \alpha \nabla J(\beta)_i.\]

随机梯度下降在R中的实现如下。

sgd.lm <- function(X, y, beta.init,
                   alpha = 0.5, n.samples = 1,
                   tol = 1e-5, max.iter = 100){
  n <- length(y)
  beta.old <- beta.init
  J <- betas <- list()
  sto.sample <- sample(1:n, n.samples, replace = TRUE)
  betas[[1]] <- beta.old
  J[[1]] <- lm.cost(X, y, beta.old)
  beta.new <- beta.old - alpha *
    sgd.lm.cost.grad(X[sto.sample, ], y[sto.sample], beta.old)
  betas[[2]] <- beta.new
  J[[2]] <- lm.cost(X, y, beta.new)
  iter <- 0
  n.best <- 0
  while ((abs(lm.cost(X, y, beta.new) -
              lm.cost(X, y, beta.old))  > tol) &
         (iter + 2 < max.iter)){
    beta.old <- beta.new
    sto.sample <- sample(1:n, n.samples, replace = TRUE)
    beta.new <- beta.old -
      alpha * sgd.lm.cost.grad(X[sto.sample, ],
                               y[sto.sample],
                               beta.old)
    iter <- iter + 1
    betas[[iter + 2]] <- beta.new
    J[[iter + 2]] <- lm.cost(X, y, beta.new)
  }
  if (abs(lm.cost(X, y, beta.new) - lm.cost(X, y, beta.old))
      > tol){
    cat('算法无法收敛。 \n')
  } else{
    cat('算法收敛\n')
    cat('共迭代',iter + 1,'次','\n')
    cat('系数估计为：', beta.new, '\n')
    return(list(coef = betas,
                cost = J,
                niter = iter + 1))
  }
}

## Make the cost function
sgd.lm.cost <- function(X, y, beta){
   n <- length(y)
   if (!is.matrix(X)){
    X <- matrix(X, nrow = 1)
  }
   loss <- sum((X%*%beta -  y)^2)/(2*n)
return(loss)
}
## Calculate the gradient
sgd.lm.cost.grad <- function(X, y, beta){
  n <- length(y)
  if (!is.matrix(X)){
    X <- matrix(X, nrow = 1)
  }
  t(X)%*%(X%*%beta - y)/n
}

现在我们在章节_3.5.1中模拟的线性回归数据中实现SGD算法。

#> 算法收敛
#> 共迭代 253 次 
#> 系数估计为： 1.157 2.95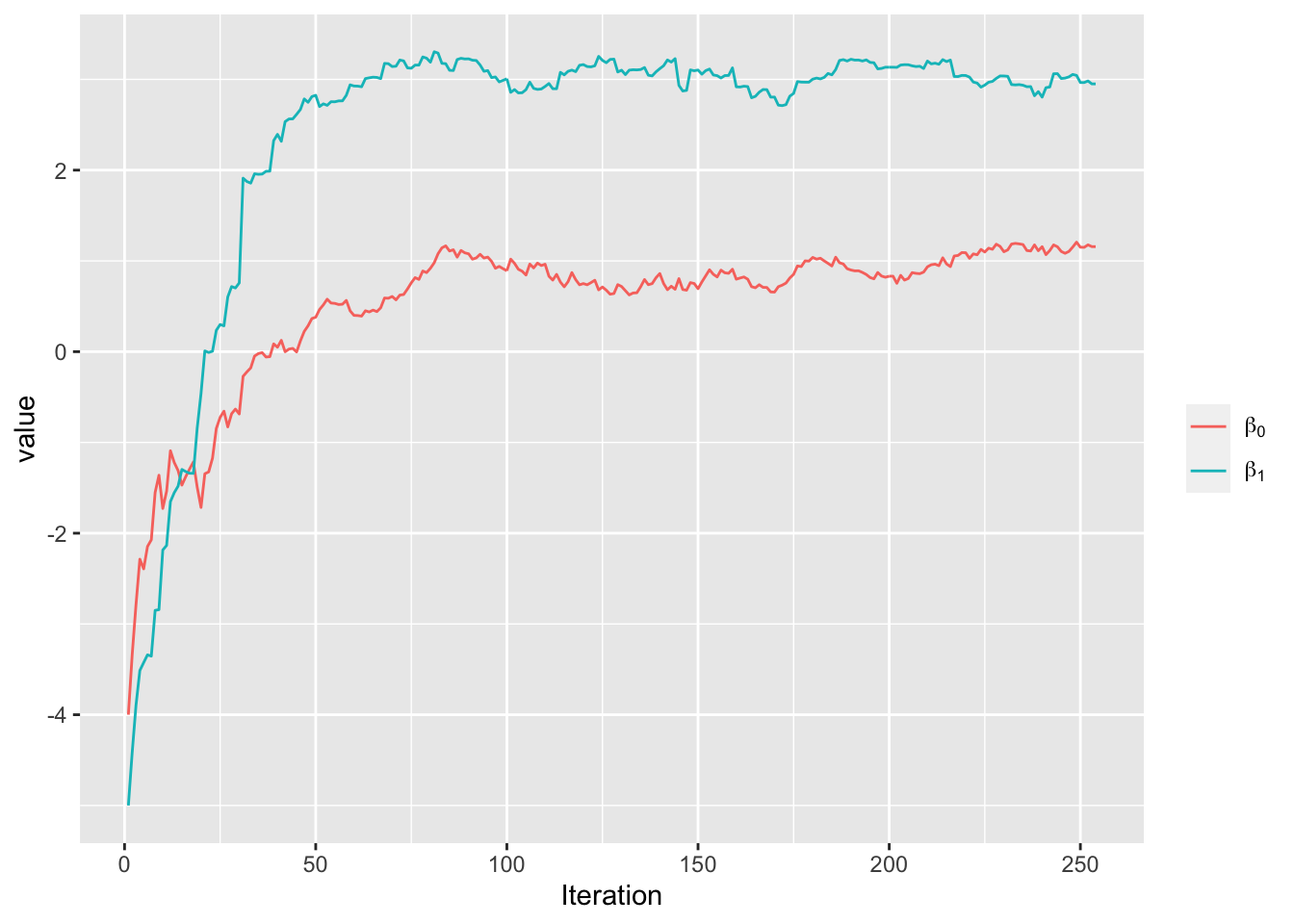

图3.7: 随机梯度下降算法的收敛情况

3.6 优化算法比较

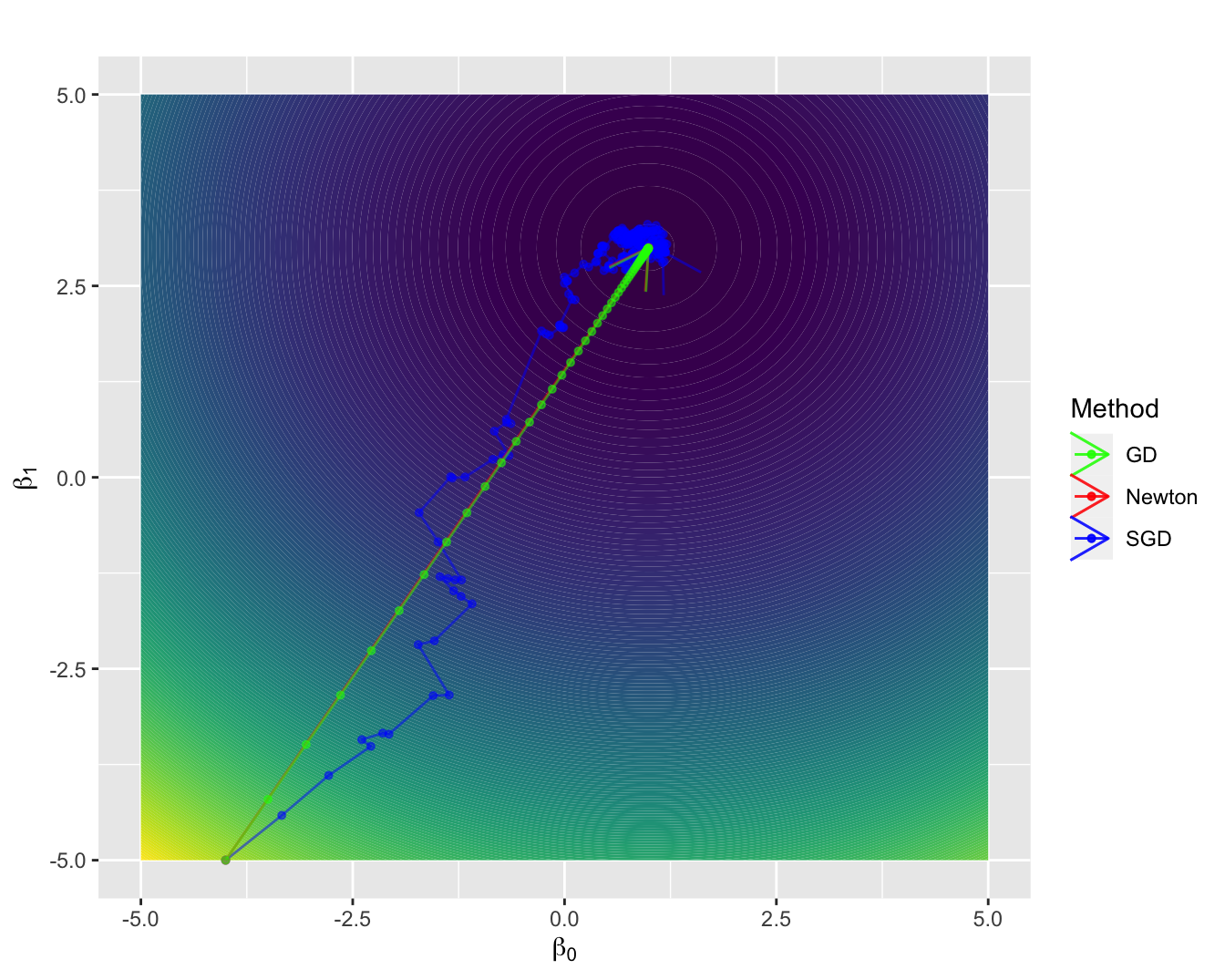
图3.8: 梯度下降算法、随机梯度下降算法和牛顿算法的收敛情况比较

基于章节_3.5.1中模拟的线性回归数据，我们来比较梯度下降算法、随机梯度下降算法和牛顿算法。从图_3.8中我们可以发现：

牛顿迭代的收敛速度很快，前提条件是海塞矩阵存在，但在复杂的机器学习方法中海塞矩阵的解析表达式通常很难求得或者无法求得。
如果训练样本的个数非常庞大，牛顿方法或者梯度下降方法可能会花费很长的时间才可以收敛，这时随机梯度下降是一个更好的选择。
随机梯度下降的收敛路径带有较多噪音，这是因为SGD的每次迭代只用了一个随机样本，为了平衡SGD带来的不确定性和GD的计算复杂度，我们可以在每步迭代时抽取少量样本，通常可以达到更加稳健的收敛，这也就是 mini-batch GD。
对于 $\alpha$ 的选择，可以参考 Bottou (2012) 和 Zeiler (2012)。

3.7 案例：心脏病预测

Logistic回归

Logistic 回归是应用最为广泛的分类算法之一，它通常用于解决二分类问题（0或1），例如垃圾邮件识别、疾病诊断等应用。Logistic 回归模型假定观测 $y$ 服从概率为 $p$的伯努利分布，该算法的模型设定如下：

\[ \hat p=g(\beta^Tx) = g(\beta_0+\beta_1x_1+\dots,\beta_kx_k) \] 其中 $g(x)=\frac{1}{1+e^{-x}}$ 为链接函数，它的主要目的是将 $\beta^Tx$从$(-\infty,+\infty)$ 映射到 $(0,1)$，当 $\hat p>0.5$ 时，$\hat y=1$，当 $\hat p<0.5$ 时，$\hat y=0$。

Logistic 回归模型常采用极大似然估计法进行估计，可以写出它的对数似然函数如下：

\[\begin{align*} L &= \mathrm{log}\left[\prod_{i=1}^np_i^{y_i}(1-p_i)^{1-y_i}\right]\\\ &=\sum_{i=1}^n\left[y_i\mathrm{log}p_i+(1-y_i)\mathrm{log}(1-p_i)\right]\\\ &=\sum_{i=1}^n\left[y_i\beta^Tx_i-\mathrm{log}(1+e^{\beta^Tx_i})\right]. \end{align*}\] 接下来我们使用本章之前讲过的随机梯度下降算法，结合实际的心脏病发病数据，进行基于 Logistic 回归模型的拟合和预测。

Logistic 回归随机梯度下降算法的 R 实现

sgd.logisticReg <- function(X, y, beta.init, alpha = 0.5,
  n.samples = 1, tol = 1e-5, max.iter = 100){
  n <- length(y)
  beta.old <- beta.init
  J <- betas <- list()
  sto.sample <- sample(1:n, n.samples, replace = TRUE)
  # sto.sample <- 1:n
  betas[[1]] <- beta.old
  J[[1]] <- sgd.logisticReg.cost(X, y, beta.old)
  beta.new <- beta.old -
    alpha * sgd.logisticReg.cost.grad(X[sto.sample, ],
                                      y[sto.sample],
                                      beta.old)
  betas[[2]] <- beta.new
  J[[2]] <- sgd.logisticReg.cost(X, y, beta.new)
  iter <- 0
  n.best <- 0

  while ((abs(sgd.logisticReg.cost(X, y, beta.new) -
              sgd.logisticReg.cost(X, y, beta.old))  > tol) &
         (iter + 2 < max.iter)){
    beta.old <- beta.new
    sto.sample <- sample(1:n, n.samples, replace = TRUE)
    beta.new <- beta.old -
      alpha * sgd.logisticReg.cost.grad(X[sto.sample, ],
                                        y[sto.sample],
                                        beta.old)
    iter <- iter + 1
    betas[[iter + 2]] <- beta.new
    J[[iter + 2]] <- sgd.logisticReg.cost(X, y, beta.new)
  }

  if (abs(sgd.logisticReg.cost(X, y, beta.new) -
          sgd.logisticReg.cost(X, y, beta.old)) > tol){
    cat('算法无法收敛。 \n')
  } else{
    cat('算法收敛\n')
    cat('共迭代',iter + 1,'次','\n')
    # cat('系数估计为：', beta.new, '\n')
    return(list(coef = betas,
                cost = J,
                niter = iter + 1))
  }
}

## Make the cost function
sgd.logisticReg.cost <- function(X, y, beta){
   n <- length(y)
   if (!is.matrix(X)){
    X <- matrix(X, nrow = 1)
   }
   p <- 1/(1+exp(-X %*% beta))
   loss <- -sum(y*log(p)+(1-y)*log(1-p))/n
return(loss)
}

## Calculate the gradient
sgd.logisticReg.cost.grad <- function(X, y, beta){
  n <- length(y)
  if (!is.matrix(X)){
    X <- matrix(X, nrow = 1)
  }
  t(X)%*%(1/(1+exp(-X%*%beta)) - y)/n
}

心脏病预测

本案例采用的数据来源于Kaggle平台，主要目标是根据吸烟数、年龄、性别、相关疾病、身体健康指数等预测病人是否会有心脏病。

hd = read.csv("data/framingham_heart_disease.csv")

拟合Logistic回归

为了加快随机梯度下降速度，对部分特征进行标准化，数据共有3656条，用其中的3000条进行训练，剩余的用作测试。

mean_norm <- function(x){
  (x-mean(x))/sd(x)
}
X <- cbind(1, as.matrix(hd[,-14]))
y <- as.matrix(hd[,14])
X[,3] <- mean_norm(X[,3])
X[,4] <- log(X[,4]+1)
X[,9:14] <- apply(X[,9:14], 2, mean_norm)

X_train <- X[1:3000,]
y_train <- y[1:3000,]
X_test <- X[3001:3656,]
y_test <- y[3001:3656,]
beta.init <- runif(14, -1, 0)

res <- sgd.logisticReg(X_train, y_train,
                      beta.init, alpha = 0.01,
                      n.samples = 1,
                      max.iter = 1000, tol = 1e-6)
#> 算法收敛
#> 共迭代 540 次

plot(1:length(res$cost), res$cost, type = "l",
  xlab = "Iterations", ylab = "Loss")

预测

p <- 1/(1+exp(-X_test%*%res$coef[[length(res$coef)]]))
y_predicted <- ifelse(p>=0.5, 1, 0)
print(paste0("accuracy:", sum(y_predicted==y_test)/656))
#> [1] "accuracy:0.836890243902439"

3.8 拓展阅读

Bottou (2012) 是实战中随机梯度下降算法通常用到的一些技巧。
Zeiler (2012) 是关于如何适应性的选择梯度下降算法和随机梯度下降算法中的 $\alpha$。

参考文献

Bottou, Léon. 2012. “Stochastic Gradient Descent Tricks.” In Neural Networks: Tricks of the Trade, 421–36. Springer.

Zeiler, Matthew D. 2012. “Adadelta: An Adaptive Learning Rate Method.” arXiv Preprint arXiv:1212.5701.

第 3 章 优化算法