第 7 章独立蒙特卡洛抽样

7.1 介绍

蒙特卡罗方法（Monte Carlo method），也称统计模拟方法，是1940年代中期由于科学技术的发展和电子计算机的发明，而提出的一种以概率统计理论为指导的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。

较早的蒙特卡洛方法的变体应该是解决布冯的针头（Buffon’s needle）问题。在该问题中，\(pi\)可以通过将针头掉落在平行等距条形地板上的方向来估计。在1930年代，恩里科·费米（Enrico Fermi）在研究中子扩散时首先进行了蒙特卡洛方法的实验，但他没有发表这项工作的成果。

20世纪40年代，在科学家冯·诺伊曼等计算机专家为美国国家实验室的核武器计划工作时，发明了蒙特卡罗方法。由当时的核武器计划属于保密项目，该成果的取名由实验室的一个计算机专家的叔叔经常在摩纳哥的蒙特卡洛赌场输钱得名，而蒙特卡罗方法正是以概率为基础的方法。与它对应的是确定性算法。冯·诺伊曼（John von Neumann）立即意识到了它的重要性。冯·诺依曼（Von Neumann）对ENIAC计算机进行了编程，以运行蒙特卡洛计算。 1946年，洛斯阿拉莫斯实验室的核武器物理学家正在研究可裂变材料中的中子扩散。当时尽管拥有大多数必要的数据，例如中子在与原子核碰撞之前在物质中行进的平均距离以及碰撞后中子可能释放出多少能量，但洛斯阿拉莫斯物理学家使用常规的数学方法解决该问题，蒙特卡洛随机实验随即被用于解决该问题。

尽管早期蒙特卡洛方法受到当时受到计算工具性能的严格限制，蒙特卡洛方法对于美国原子弹计划曼哈顿项目所需的仿真至关重要。在1950年代，之后该方法被用于与氢弹研制有关的早期工作，并在物理学，物理化学和运筹学领域得到普及。美国的兰德公司和美国空军是这段期间负责资助和传播有关蒙特卡洛方法的两个主要组织。之后它开始在许多不同领域中得到广泛应用。现代蒙特卡罗方法在金融工程学、宏观经济学、生物医学、计算物理学（如粒子输运计算、量子热力学计算、空气动力学计算）、机器学习等领域应用广泛。

7.2 直接抽样

假设已知随机变量 \(U\) 服从均匀分布： \(U\sim U(0,1)\)，随机变量 \(X\) 的分布函数为 \(F(x)\)，设 \(Y = F_X^{-1}(U)\)，我们可以得到：

\[ F_{Y}(y)=\mathbb{P}(Y \leq y)=\mathbb{P}\left(F_{X}^{-1}(U) \leq y\right)=\mathbb{P}\left(U \leq F_{X}(y)\right)=F_{X}(y). \] 也就是说 \(Y\) 和 \(X\) 具有同样的概率分布。这样的话，如果我们可以抽取均匀分布的随机数的话，在 \(F_X^{-1}\) 存在的条件下，我们就可以产生任何连续随机变量 \(X\) 的随机数。这种对连续随机变量 \(X\) 抽样的方法叫作直接抽样（也叫逆方法，或逆分布函数变换法）。

我们也可以从另外一个角度考虑这个问题，因为对任何的连续随机变量\(X\)， \(F_X(X) \sim U(0, 1)\)，所以直接抽样也就是先从 \(U\sim U(0,1)\) 中抽样后再代入 \(F_X^{-1}\)。

例3.1 如果 \(X \sim \exp(\lambda)\)，我们有

\[F_{X}(x)=\left\{\begin{array}{ll}{0} & {\text { for } x<0;} \\ {1-e^{-\lambda x}} & {\text { for } x \geq 0.}\end{array}\right.\]假设 \(\lambda = 1\)，那么我们如何从指数分布中实现直接抽样？

lambda <- 1
u <- runif(20)
x <- -1/lambda * log(1 - u)
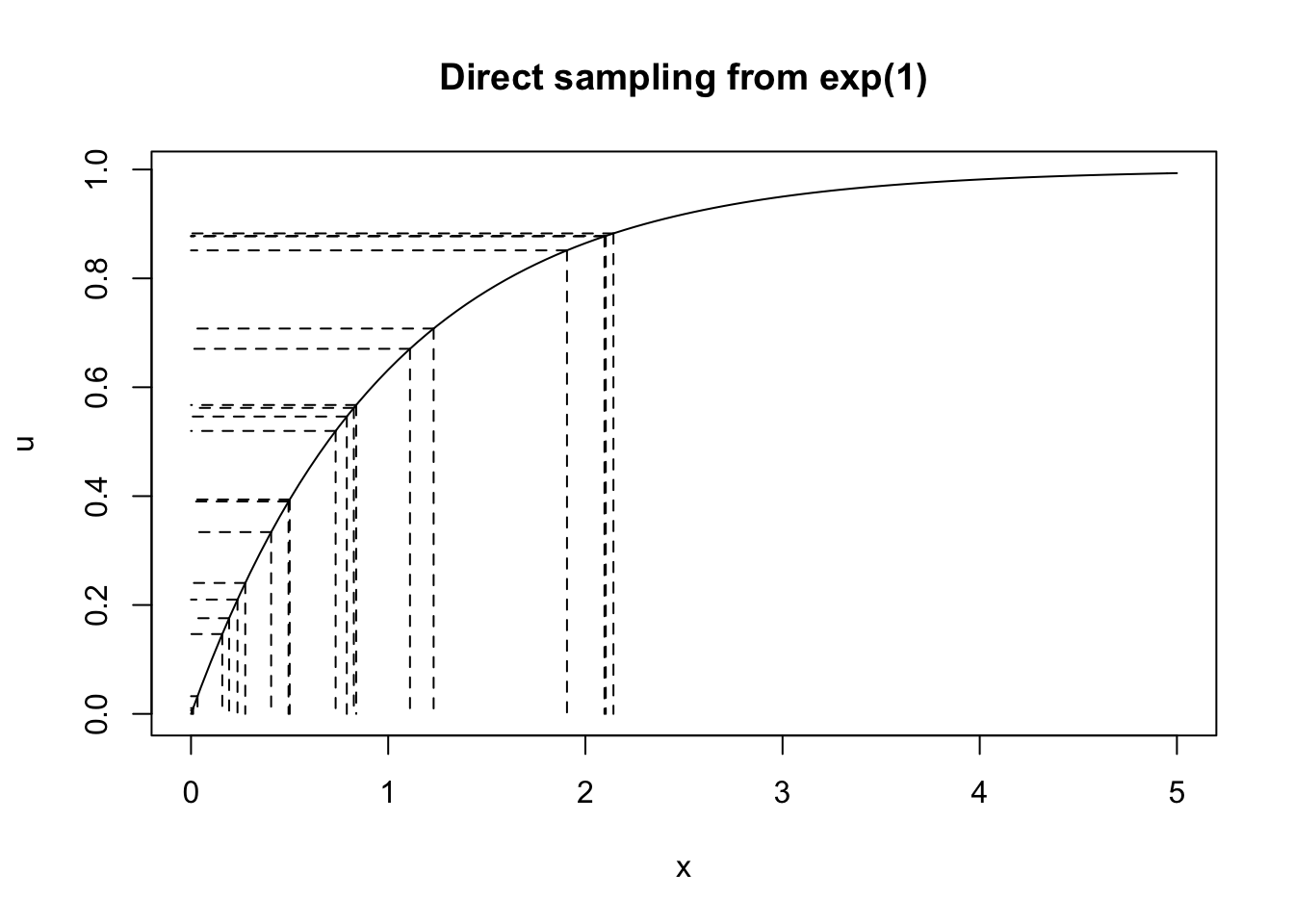
curve(1 - exp(-x), 0, 5, ylab = 'u',
      main = 'Direct sampling from exp(1)')
for (i in 1:length(x)){
  lines(c(x[i], x[i]), c(u[i], 0), lty = 'dashed')
  lines(c(x[i], 0), c(u[i], u[i]), lty = 'dashed')
}

7.3 拒绝抽样

7.3.1 拒绝抽样的思想

假设我们想抽取服从 \(f(x)\) 的随机变量 \(X\) 的随机数，且我们无法计算 \(F^{-1}_X\)，这时候拒绝抽样是一种可行的抽样方法。

拒绝抽样的思想是：如果我们难以从 \(f(x)\) 中抽样，我们可以从一个易于抽样的概率密度 \(g(x)\) 中抽样，然后通过选择接受或者拒绝 \(g(x)\) 的抽样来使得被接受的样本的概率分布服从 \(f(x)\)，从而得到了来自 \(f(x)\) 的随机数。这里我们把 \(g(x)\) 称作 猜想概率密度，\(f(x)\) 称作 目标概率密度。

这里的猜想概率密度 \(g(x)\) 需要满足两个条件：

\(\mathcal{X}_f \subset \mathcal{X}_g\)，其中 \(\mathcal{X}_f\) 为 \(f(x)\) 的支集（对应的随机变量可能取到的值的集合，对应英文里的 support）， \(\mathcal{X}_g\) 为 \(g(x)\) 的支集。如果 \(f(x)\) 的支集中存在有 \(g(x)\) 取不到的区域，那么这个区域就无法得到对应的抽样，这种情况下 \(g(x)\) 作为猜想概率密度就是不合理的。
\(\frac{f(x)}{g(x)}\) 是有界的，也就是说，对于 \(\mathcal{X}_f\) 任意 \(x\)，都有 \(\frac{f(x)}{g(x)} \leq M\)。这等价于：\[M=\sup _{x \in \mathcal{X}_{f}} \frac{f(x)}{g(x)}<\infty.\]

满足这两个条件的 \(g(x)\) 最简单的选择就是一个比 \(f(x)\) 更加厚尾的分布。

7.3.2 拒绝抽样算法

拒绝抽样算法 (Rejection Sampling)

从 \(g(x)\) 中抽取随机数 \(x\)。
计算接受概率 \[\alpha = \frac{f(x)}{M g(x)}.\]
产生均匀分布的随机数 \(U \sim U(0,1)\)。如果 \(U \leq \alpha\)，接受 \(x\)，否则拒绝 \(x\)。如果拒绝，则返回第1步。也就是说，以 \(\alpha = \frac{f(x)}{M g(x)}\) 为接受概率来接受第2步中抽取的随机数 \(x\)。

重复以上过程直到得到目标数目的服从分布 \(f(x)\) 的随机数。在拒绝抽样中，所有被接受的随机数的概率分布应该服从 \(f(x)\)。

例2.1 以自由度为 \(2\) 的 \(t_2\) 分布为猜想概率密度，使用拒绝抽样算法抽取正态分布 \(N(0,1)\) 的随机数。

我们先来看一下 \(N(0, 1\) 和 \(t_2\) 的概率密度函数。如图_7.1，\(t_2\) 比 \(N(0,1)\) 更加厚尾，所以可以作为猜想概率密度。

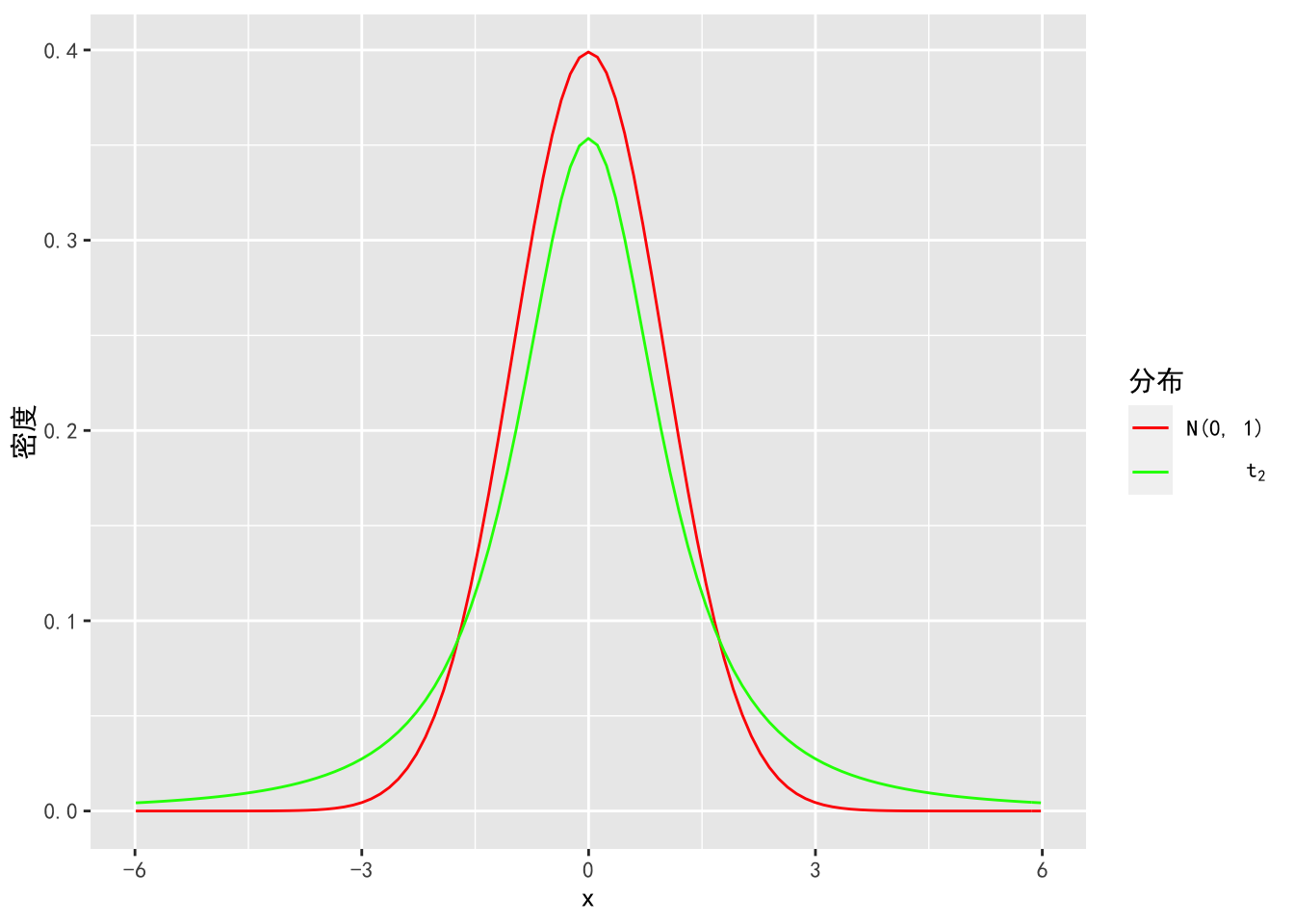
图7.1: \(N(0,1)\) 和 \(t_2\) 分布的概率密度函数

根据拒绝抽样算法的步骤，我们可以通过以下过程来抽取标准正态分布的随机数。

iter <- 10000
k <- 0
X <- vector()

# 计算 M
fg <- function(x){dnorm(x)/dt(x, df = 2)}
M <- optim(1, fg, method = 'BFGS',
           control = list(fnscale = -1))$value

# 拒绝抽样
for (i in seq_len(iter)){
  u <- runif(1)
  x <- rt(1, 2)
  alpha <- dnorm(x)/(dt(x, df = 2) * M)
  if (u <= alpha){
    X[k] <- x
    k <- k + 1
  }
}

# 计算接受概率
cat('接受概率为', k/iter, ' \n')
#> 接受概率为 0.8015
cat('1/M = ', 1/M, ' \n')
#> 1/M =  0.7953

# 直方图
hist(X, prob = TRUE)
curve(dnorm, add = TRUE, col = "red")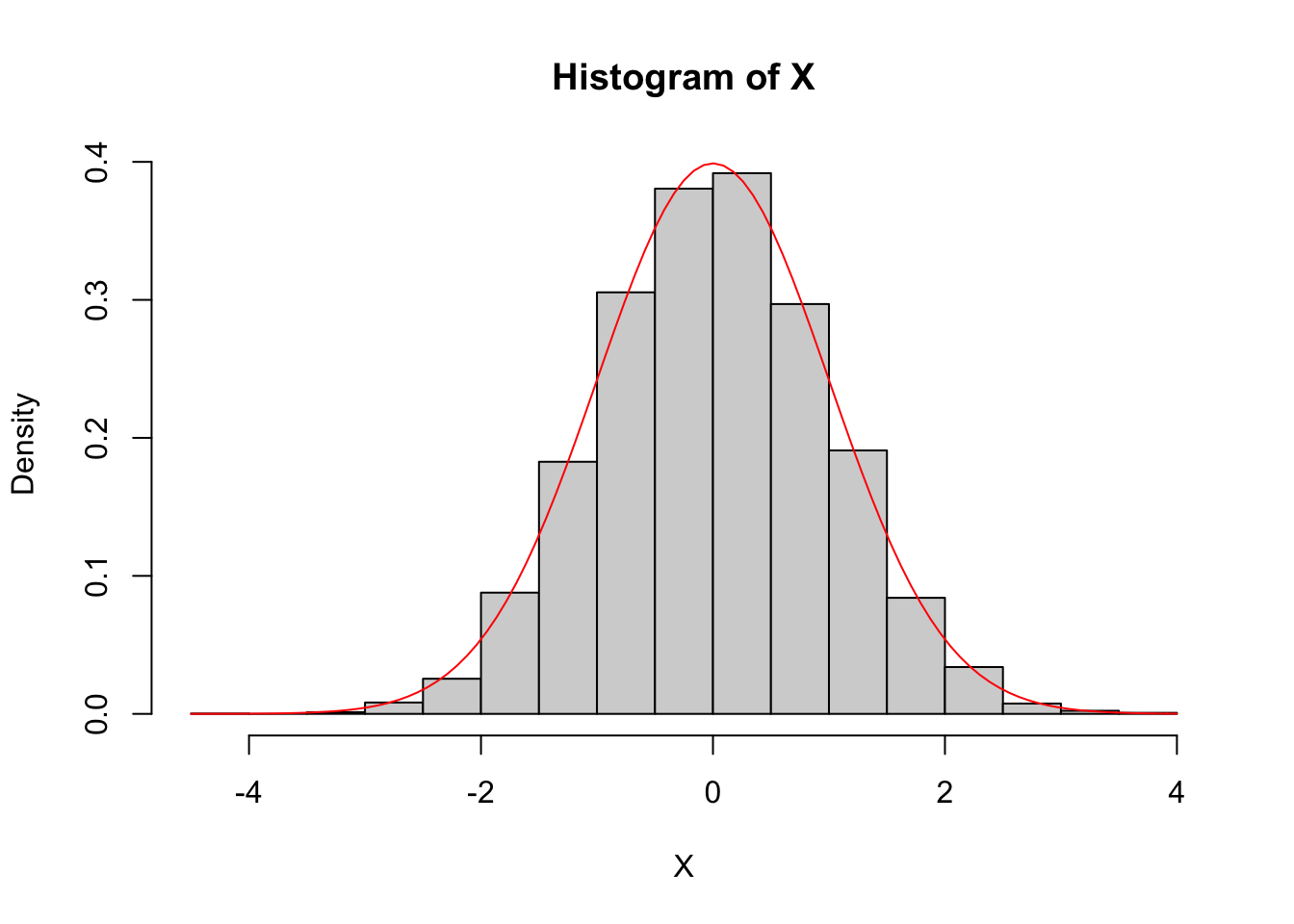

7.3.3 拒绝抽样的性质

拒绝抽样的性质之一为：在整个抽样过程中，所有抽取的随机数被接受的概率为 \(\frac{1}{M}\)，我们可以通过以下推导得到 (Peng 2018)。

\[\begin{aligned} \mathbb{P}(x \text { 被接受}) &=\mathbb{P}\left(U \leq \frac{f(x)}{M g(x)}\right) \\ &=\int \mathbb{P}\left(U \leq \frac{f(x)}{M g(x)} |x \right) g(x) d x \\ &=\int \frac{f(x)}{M g(x)} g(x) d x \\ &=\frac{1}{M} \end{aligned}.\] 这个性质可以为我们选择猜想概率密度 \(g(x)\) 提供一定的参考依据。理论上讲，任何的概率密度只要满足 \(\mathcal{X}_f \subset \mathcal{X}_g\) 都可以作为猜想概率密度，但在实际中，我们应该选择一个与 \(f(x)\) 尽可能接近的概率密度作为 \(g(x)\)，这样的话我们才可以得到尽可能大的接受概率，从而提高抽样效率。在例5.2 中，我们也可以看出接受概率和 \(\frac{1}{M}\) 非常接近。

拒绝抽样的第二个性质为：被接受的随机数服从目标概率密度 \(f(x)\)，也就是说被接受的随机数的分布函数为 \(F(x) = \int_{-\infty}^t f(x) dx\)，我们可以通过以下推导得到 (Peng 2018)。

\[\begin{aligned} \mathbb{P}(X \leq t | X \text { 被接受}) &=\frac{\mathbb{P}(X \leq t, X \text { 被接受})}{\mathbb{P}(X \text { 被接受 })} \\ &=\frac{\mathbb{P}(X \leq t, X \text { 被接受})}{1 / M} \\ &=M \mathbb{E}_{g} \mathbb{E}\left[\mathcal{I}\{x \leq t\} \mathcal{I}\left\{U \leq \frac{f(x)}{M g(x)}\right\} | X=x\right] \\ &=M \mathbb{E}_{g}\left[\mathcal{I}\{X \leq t\} \mathbb{E}\left[\mathcal{I}\left\{U \leq \frac{f(x)}{M g(x)}\right\} | X=x\right]\right] \\ &=M \mathbb{E}_{g}\left[\mathcal{I}\{X \leq t\} \frac{f(X)}{c g(X)}\right] \\ &=\int_{-\infty}^{\infty} 1\{x \leq t\} \frac{f(x)}{g(x)} g(x) d x \\ &=\int_{-\infty}^{t} f(x) d x \\ &=F(t) \end{aligned}.\]

几点注意

7.4 重要性抽样

参考文献

Peng, Roger D. 2018. “Advanced Statistical Computing.” Work in Progress. https://bookdown.org/rdpeng/advstatcomp/.

第 7 章 独立蒙特卡洛抽样