Introduction to Optimization¶

Feng Li

School of Statistics and Mathematics

Central University of Finance and Economics

feng.li@cufe.edu.cn

https://feng.li/statcomp

Motivation: Why Optimize?¶

Optimization in Business¶

  • Many problems in business require something to be minimized or maximized

    • Maximizing Revenue

    • Minimizing Costs

    • Minimizing Delivery Time

    • Maximizing Financial Returns

Input and output¶

  • For many of these problems there is some control over the input

    • Maximizing Revenue - Price

    • Minimizing Costs - Number of Workers

    • Minimizing Delivery Time - Driving Route

    • Maximizing Financial Returns - Portfolio weights

Optimization in Statistics¶

  • In statistics, many estimators maximize or minimize a function

    • Maximum Likelihood

    • Least Squares

    • Method of Moments

    • Posterior Mode

  • Suppose we want to find an minimum or maximum of a function $f(x)$

  • Sometimes $f(x)$ will be very complicated

  • Are there computer algorithms that can help?

  • YES!

    • Newton’s Method

    • Quasi-Newton

    • Nelder Mead

Newton’s Method¶

Finding a root¶

  • Consider the problem of finding the root or zero a function.

  • For the function $g(x)$ the root is the point $x^*$ such that $g(x^*)=0$

  • An algorithm for solving this problem was proposed by Newton and Raphson nearly 500 years ago.

  • We will use this algorithm to find the root of $g(x)=3x^5-4x^4+6x^3+4x-4$

In [4]:
gx<-function(x){
  y=(3*(x^5))-(4*(x^4))+(6*(x^3))+(4*x)-4
  return(y)  
}

dgx<-function(x){
  y=(15*(x^4))-(16*(x^3))+(18*(x^2))+4
  return(y)  
}
In [12]:
gridx<-seq(-2,2,0.01)
gridy<-gx(gridx)
plot(gridx,gridy,"l",main='Root Finding', ylim= c(-200, 100), 
     xlab = 'x', ylab=expression(y=3*x^5-4*x^4+6*x^3+4*x-4))
lines(c(-2,2),c(0,0))

Finding the Tangent¶

  • To find the tangent evaluate the first derivative of $g(x)$.

  • The function is $$g(x)=3x^5-4x^4+6x^3+4x-4$$

  • The first derivative is $$g'(x)=15x^4-16x^3+18x^2+4$$

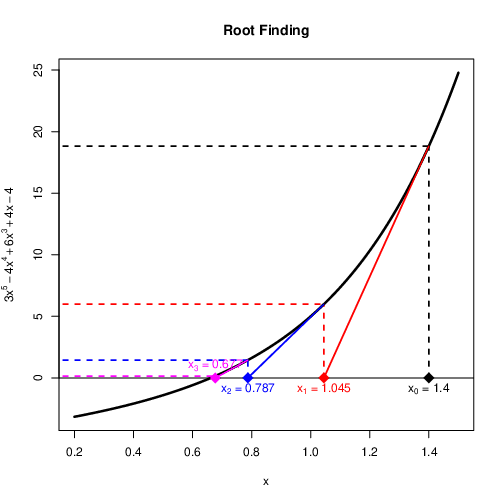
rootfinding

Find the crossing point¶

  • Find the crossing point From basic Geometry
$$g'(x_0)=\frac{g(x_0)}{x_0-x_1}$$
  • Rearrange
$$\begin{aligned} x_0-x_1&=\frac{g(x_0)}{g'(x_0)}\\ -x_1&=-x_0+\frac{g(x_0)}{g'(x_0)}\\ x_1&=x_0-\frac{g(x_0)}{g'(x_0)} \end{aligned}$$

Stopping Rule¶

  • With each step the algorithm should get closer to the root.

  • However, it can run for a long time without reaching the exact root

  • There must be a stopping rule otherwise the program could run forever.

  • Let $\epsilon$ be an extremely small number e.g. $1\times 10^{-10}$ called the tolerance level

  • If $|g(x^*)|<\epsilon$ then the solution is close enough and there is a root at $x^*$

Newton-Raphson algorithm for root finding¶

  1. Select initial value $x_0$ and set $n=0$

  2. Set $x_{n+1}=x_{n}-\frac{g(x_n)}{g'(x_n)}$

  3. Evaluate $|g(x_{n+1})|$

    • If $|g(x_{n+1})|\leq\epsilon$ then stop.

    • Otherwise set $n=n+1$ and go back to step 2.

Your task: Write R/Python code to find the root¶

$g(x)=3x^5-4x^4+6x^3+4x-4$

Tips:

  • Write functions for $g(x)$ and $g'(x)$ first.

  • These can be inputs into a function that carries out the Newton Raphson method. Code should be flexible.

  • Use loops!

Your task: a different target function¶

  • Now use your Newton-Raphson code to find the root of $g(x)=\sqrt{|x|}$

  • The derivative has two parts $$g'(x)=\left{

        \begin{array}{l}
      1/(2\sqrt{x})\quad\mbox{if $x>0$}\\
      -1/(2\sqrt{-x})\quad\mbox{if $x<0$}
    \end{array}
  \right.$$

  • Use 0.25 as the starting value.

Learn from mistakes¶

  • Newton-Raphson does not always converge

  • Be careful using while. Avoid infinite loops.

  • Don’t always assume the answer given by code is correct. Check carefully!

  • Print warning messages in code

  • For some functions, using some certain starting values leads to a series that converges, while other starting values lead to a series that diverges

  • For other functions different starting values converge to different roots.

  • Be careful when choosing the initial value.

  • Newton-Raphson doesn’t work if the first derivative is zero.

  • When can this happen?

Rough Proof of Quadratic Convergence¶

  • Can we prove anything about the rate of convergence for the Newton Raphson Method?

  • To do so requires the Taylor Series

  • Let $f(x)$ have a root at $\alpha$. The Taylor approximation states that

    $$f(\alpha)\approx f(x_n)+f'(x_n)(\alpha-x_n)+\frac{1}{2}f''(x_n)(\alpha-x_n)^2$$

  • The quality of the approximation depends on the function and how close $x_n$ is to $\alpha$

  • Since $\alpha$ is a root, $f(\alpha)=0$ This implies

    $$0\approx f(x_n)+f'(x_n)(\alpha-x_n)+\frac{1}{2}f''(x_n)(\alpha-x_n)^2$$

  • Dividing by $f'(x_n)$ and rearranging gives: $$\frac{f(x_n)}{f'(x_n)}+(\alpha-x_n)\approx\frac{-f''(x_n)}{2f'(x_n)}(\alpha-x_n)^2$$

  • More rearranging $$\alpha-\left(x_n-\frac{f(x_n)}{f'(x_n)}\right)\approx\frac{-f''(x_n)}{2f'(x_n)}(\alpha-x_n)^2$$

  • The term in brackets on the left hand side is the formula used to update $x$ in the Newton Raphson method $$(\alpha-x_{n+1})\approx\frac{-f''(x_n)}{2f'(x_n)}(\alpha-x_n)^2$$

  • This can be rewritten in terms of errors $e_{n+1}=\alpha-x_{n+1}$ and $e_n=\alpha-x_n$ $$e_{n+1}\approx\frac{-f''(x_n)}{2f'(x_n)}e_n^2$$

Conclusion¶

  • Why did we spend so much time on finding roots of an equation?

  • Isn’t this topic meant to be about optimization?

  • Can we change this algorithm slightly so that it works for optimization?