{
 "cells": [
  {
   "cell_type": "markdown",
   "id": "c57b2ce5",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "# Sampling From Unknown Distributions\n",
    "\n",
    "\n",
    "Feng Li\n",
    "\n",
    "School of Statistics and Mathematics\n",
    "\n",
    "Central University of Finance and Economics\n",
    "\n",
    "[feng.li@cufe.edu.cn](mailto:feng.li@cufe.edu.cn)\n",
    "\n",
    "[https://feng.li/statcomp](https://feng.li/statcomp)\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 1,
   "id": "69326237",
   "metadata": {
    "slideshow": {
     "slide_type": "skip"
    }
   },
   "outputs": [],
   "source": [
    "options(jupyter.plot_scale=0.8)"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "47a7f101",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "## Direct Methods\n",
    "\n",
    "- Only need random numbers from uniform\n",
    "\n",
    "- Assume that we have a way to simulate from a uniform distribution between $0$ and $1$, $u\\sim U(0,1)$\n",
    "\n",
    "- If this is available, it is possible to simulate many other probability distributions.\n",
    "\n",
    "- The most simple method is the **Direct Method**"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "b5ca565a",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
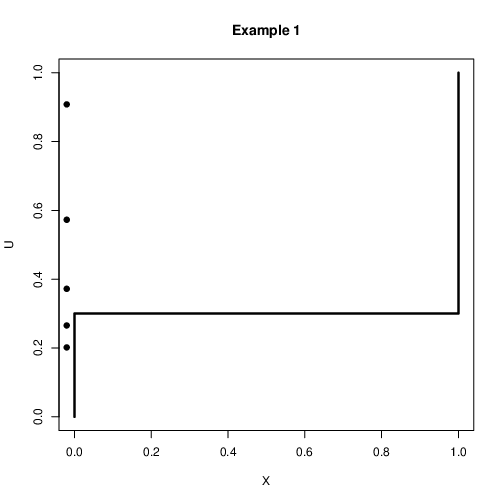
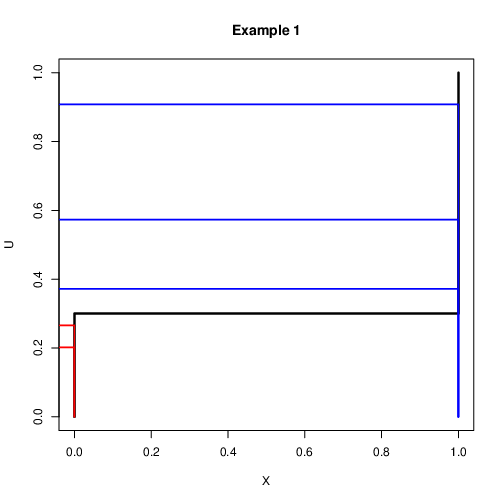
   "source": [
    "### Discrete Case: Example 1\n",
    "\n",
    "-   Assume that we want to simulate a binary variable $X$ with\n",
    "    $\\mbox{Pr}(X=1)=0.3$ and $\\mbox{Pr}(X=0)=0.7$\n",
    "\n",
    "-   Let $u\\sim U(0,1)$. Then the following rule can be used\n",
    "    $$x=\\left\\{\\begin{array}{c}\n",
    "                     1 \\quad \\mbox{if $u<0.3$}\\\\\n",
    "                     0 \\quad \\mbox{if $u>0.3$}\\\\\n",
    "                   \\end{array}\n",
    "                 \\right.$$\n",
    "\n",
    "-   It is expected that if this is repeated many times 30% $X=1$ and 70%\n",
    "    $X=0$"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 2,
   "id": "df9d4801",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "outputs": [
    {
     "data": {
      "text/html": [
       "<style>\n",
       ".list-inline {list-style: none; margin:0; padding: 0}\n",
       ".list-inline>li {display: inline-block}\n",
       ".list-inline>li:not(:last-child)::after {content: \"\\00b7\"; padding: 0 .5ex}\n",
       "</style>\n",
       "<ol class=list-inline><li>0</li><li>0</li><li>1</li><li>1</li><li>0</li><li>1</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>1</li><li>0</li><li>0</li><li>0</li><li>1</li><li>0</li><li>1</li><li>1</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>1</li><li>1</li><li>0</li><li>1</li><li>0</li><li>0</li><li>0</li><li>0</li><li>1</li><li>0</li><li>0</li><li>0</li><li>1</li><li>1</li><li>1</li><li>1</li><li>1</li><li>0</li><li>0</li><li>0</li><li>1</li><li>0</li><li>0</li><li>1</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>1</li><li>0</li><li>1</li><li>0</li><li>0</li><li>0</li><li>0</li><li>0</li><li>1</li><li>0</li><li>0</li><li>1</li><li>0</li><li>0</li><li>1</li><li>0</li><li>0</li><li>1</li><li>0</li><li>0</li><li>0</li><li>1</li><li>1</li><li>0</li><li>0</li><li>1</li><li>1</li><li>0</li><li>1</li></ol>\n"
      ],
      "text/latex": [
       "\\begin{enumerate*}\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 1\n",
       "\\item 1\n",
       "\\item 1\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\item 1\n",
       "\\item 0\n",
       "\\item 1\n",
       "\\end{enumerate*}\n"
      ],
      "text/markdown": [
       "1. 0\n",
       "2. 0\n",
       "3. 1\n",
       "4. 1\n",
       "5. 0\n",
       "6. 1\n",
       "7. 0\n",
       "8. 0\n",
       "9. 0\n",
       "10. 0\n",
       "11. 0\n",
       "12. 0\n",
       "13. 0\n",
       "14. 0\n",
       "15. 0\n",
       "16. 0\n",
       "17. 0\n",
       "18. 1\n",
       "19. 0\n",
       "20. 0\n",
       "21. 0\n",
       "22. 1\n",
       "23. 0\n",
       "24. 1\n",
       "25. 1\n",
       "26. 0\n",
       "27. 0\n",
       "28. 0\n",
       "29. 0\n",
       "30. 0\n",
       "31. 0\n",
       "32. 0\n",
       "33. 1\n",
       "34. 1\n",
       "35. 0\n",
       "36. 1\n",
       "37. 0\n",
       "38. 0\n",
       "39. 0\n",
       "40. 0\n",
       "41. 1\n",
       "42. 0\n",
       "43. 0\n",
       "44. 0\n",
       "45. 1\n",
       "46. 1\n",
       "47. 1\n",
       "48. 1\n",
       "49. 1\n",
       "50. 0\n",
       "51. 0\n",
       "52. 0\n",
       "53. 1\n",
       "54. 0\n",
       "55. 0\n",
       "56. 1\n",
       "57. 0\n",
       "58. 0\n",
       "59. 0\n",
       "60. 0\n",
       "61. 0\n",
       "62. 0\n",
       "63. 0\n",
       "64. 0\n",
       "65. 0\n",
       "66. 0\n",
       "67. 0\n",
       "68. 0\n",
       "69. 0\n",
       "70. 0\n",
       "71. 0\n",
       "72. 1\n",
       "73. 0\n",
       "74. 1\n",
       "75. 0\n",
       "76. 0\n",
       "77. 0\n",
       "78. 0\n",
       "79. 0\n",
       "80. 1\n",
       "81. 0\n",
       "82. 0\n",
       "83. 1\n",
       "84. 0\n",
       "85. 0\n",
       "86. 1\n",
       "87. 0\n",
       "88. 0\n",
       "89. 1\n",
       "90. 0\n",
       "91. 0\n",
       "92. 0\n",
       "93. 1\n",
       "94. 1\n",
       "95. 0\n",
       "96. 0\n",
       "97. 1\n",
       "98. 1\n",
       "99. 0\n",
       "100. 1\n",
       "\n",
       "\n"
      ],
      "text/plain": [
       "  [1] 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 1 0 0 0 0 0 0 0 1 1 0 1 0\n",
       " [38] 0 0 0 1 0 0 0 1 1 1 1 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1\n",
       " [75] 0 0 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 1 1 0 0 1 1 0 1"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "u = runif(100)\n",
    "x = ifelse(u<0.3, yes=1, no=0)\n",
    "x"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "6b9cd3e4",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "![image](figures/d1p1.png) "
   ]
  },
  {
   "cell_type": "markdown",
   "id": "95e0a296",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "![image](figures/d1p3.png) "
   ]
  },
  {
   "cell_type": "markdown",
   "id": "f5b146bd",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
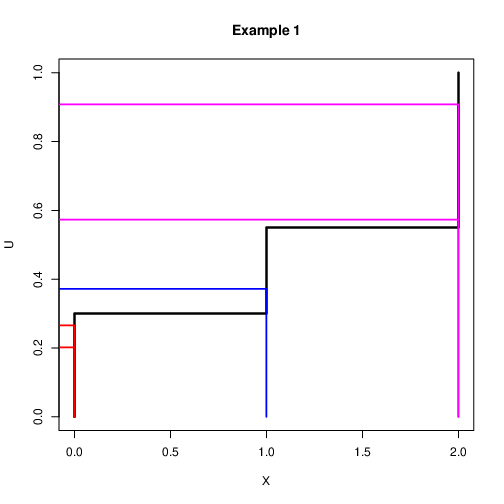
   "source": [
    "### Discrete Case: Example 2\n",
    "\n",
    "-   Assume that we want to **simulate a discrete variable $X$ with\n",
    "    probability** $\\mbox{Pr}(X=0)=0.3$ and $\\mbox{Pr}(X=1)=0.25$ and\n",
    "    $\\mbox{Pr}(X=2)=0.45$\n",
    "\n",
    "-   Let $u\\sim U(0,1)$. Then the following rule can be used\n",
    "    $$x=\\left\\{\\begin{array}{l}\n",
    "                            0 \\quad \\mbox{if $u<0.3$}\\\\\n",
    "                            1 \\quad \\mbox{if $0.3<u<0.55$}\\\\\n",
    "                            2 \\quad \\mbox{if $u>0.55$}\n",
    "                          \\end{array}\n",
    "                        \\right.$$\n",
    "\n",
    "-   It is expected that if this is repeated many times, roughly 30%\n",
    "    $X=0$, 25% $X=1$ and 45% $X=2$"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "e6617d2b",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "![image](figures/d2p3.png) "
   ]
  },
  {
   "cell_type": "markdown",
   "id": "88814415",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
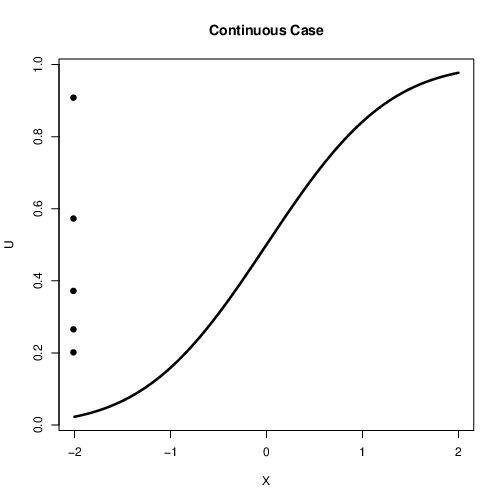
   "source": [
    "### Continuous Case\n",
    "\n",
    "-   How do we extend this idea to the continuous case?\n",
    "\n",
    "-   What was the step function in our discrete example?\n",
    "\n",
    "-   It is the **cumulative distribution function (CDF)**\n",
    "\n",
    "-   Can we replace the discrete cdf with a continuous cdf?\n",
    "\n",
    "-   Yes!"
   ]
  },
  {
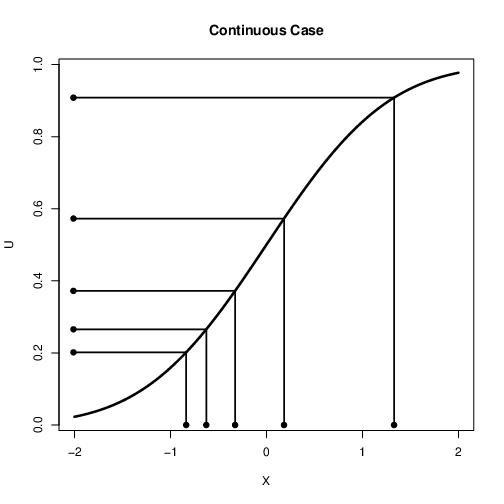
   "cell_type": "markdown",
   "id": "27dfe1db",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "![image](figures/cp1.png) "
   ]
  },
  {
   "cell_type": "markdown",
   "id": "f704e110",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "![image](figures/cp3.png) "
   ]
  },
  {
   "cell_type": "markdown",
   "id": "11721518",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "\n",
    "### Continuous Case\n",
    "\n",
    "-   The cdf, $F(X)$ takes values of $X$ and gives a value between $0$\n",
    "    and $1$\n",
    "\n",
    "-   Here we take values between $0$ and $1$ and get a value of $X$\n",
    "\n",
    "-   What function do we use?\n",
    "\n",
    "-   We use the **Inverse cdf**"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "c5b5b89f",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "### Continuous Case: Direct Methods\n",
    "\n",
    "#### Probability Integral Transform\n",
    "\n",
    "-   If $Y$ is a continuous random variable with cdf $F(y)$ , then the\n",
    "    random variable $F_y^{-1}(U)$, where $U \\sim uniform(O, 1)$, has\n",
    "    distribution $F(y)$.\n",
    "\n",
    "-   **Example:** If $Y \\sim exponential(A)$, then the probability\n",
    "    density function (PDF) is\n",
    "    $$f(x;\\lambda) = \\begin{cases} \\lambda e^{-\\lambda x} & x \\ge 0, \\\\ 0 & x < 0. \\end{cases}$$\n",
    "    and the cumulative distribution function (CDF) is given by\n",
    "    $$F(x;\\lambda) = \\begin{cases} 1-e^{-\\lambda x} & x \\ge 0, \\\\ 0 & x < 0. \\end{cases}$$\n",
    "    Then $$F_Y^{-1}(U) = -\\log(1-U)/\\lambda$$ is an exponential random\n",
    "    variable.\n",
    "\n",
    "-   Thus, if we generate $U_1,..., U_n$ as iid uniform random variables,\n",
    "    $-\\lambda (1-U_i)$, are iid exponential random variables with\n",
    "    parameter $\\lambda$."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 3,
   "id": "cc4dc294",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "outputs": [],
   "source": [
    "u2x <- function(u, lambda)\n",
    "    {\n",
    "        x <- - log(1-u)/lambda\n",
    "        return(x)\n",
    "    }\n",
    "\n",
    "rmyexp <- function(n, lambda)\n",
    "    {\n",
    "        u <- runif(n, 0, 1)\n",
    "        x <- u2x(u, lambda)\n",
    "        return(x)\n",
    "    }"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 4,
   "id": "dcb56859",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeAAAAFoCAIAAAAAVb93AAAACXBIWXMAABJ0AAASdAHeZh94\nAAAgAElEQVR4nO3daVQUZ7oH8KfoBRBoNgGb1QTFDbeowSgIThw1TDxGcxMnMImY6MH1ZNPR\nGTUxmsRcl+R6jluiY9REOTnJmHEbY8xoNIpDJipKaxTBDVwQhAZEoenuuh+KKTuILL1UvdX8\nfycf3n6rinqCT/+prq6u5nieJwAAYI+H3AUAAEDTENAAAIxCQAMAMAoBDQDAKAQ0AACjENAA\nAIxCQAMAMAoBDQDAKAQ0AACjENAAAIxCQAMAMAoBDQDAKAQ0AACjENAAAIxCQAMAMAoBDQDA\nKAQ0AACjENAAAIxCQAMAMAoBDQDAKAQ0AACjENAAAIxCQAMAMAoBDQDAKAQ0AACjENAAAIxC\nQAMAMAoBDQDAKAQ0AACjENAAAIxCQAMAMAoBDQDAKAQ0AACjENAAAIxCQAMAMAoBDQDAKAQ0\nAACjENAAAIxCQAMAMAoBDQDAKAQ0AACjENAAAIxCQAMAMAoB7XJWq1XuEgBAkRDQ9njvvfc4\njuM4rmvXrkT07bff9u/fv1u3bkT05ptvCouSkpLOnDkzdOhQtVrt6enZu3fvzz//nIjq6uo+\n+OCDlJQUf3//Ll26vPrqqzdv3hR+7KRJk4Rt1Wp1RUWF7R6fe+45YdHvf/97cfL06dOTJ08e\nMGCAr69vly5dJkyYkJ2dLS7NyclRqVRiMeL8G2+8wf3Xp59+SkRTpkwRHg4fPrympubNN9+M\njIz09vaOj49///336+rqXPirBGVq5ikgQHM6Bw9tt2jRIuG316VLly+//JLjOCLq3Lkzz/Nv\nvPGGsCgqKiogIKDRb3vFihXDhw9vNBkREWE0GnmeP3DggDi5fft2cXcmk8nPz0+Y37BhgzD5\n8ccfa7Xah/9B//znP1utVmGdt99+W5zftWsXz/NXrlwRt0pJSRHWnDx5sjCTmJiYmJjY6Af2\n6dPnwoULEv+GgXHNPAV4NKfzIKDtIXZnWFhYcHCwMG4U0AIfH58OHTo83KkdO3a0fbh48WKe\n581mc6dOnYSZtLQ0cXc//vijMKnRaO7cucPz/P79+8VthwwZMmnSpEGDBokzK1asEDa8d+9e\nly5dhMn4+HiLxTJx4kThYYcOHQoKCoTVxOeA8DTjOK5z585qtVr8gSNGjJD6Vwxsa+YpgOZ0\nIgS0PcTuJCKtVjtt2rQNGzYIx7y2Ab1w4UKLxVJTUzNz5kxxMjo6+vz58zzPnzlzxtfXV5gc\nN26c8JNff/11YSYwMLC+vl6YnDdvnjCZmprK87zZbO7Zs6cws2DBArGqBQsWCJO+vr5CjvM8\nf/jwYaGziWjOnDkeHg0ntT7++GNxQ/E5QER9+vS5cuUKz/MVFRUjR44U548fPy7FbxYU4lFP\nATSncyGg7WHbnTt27LBdJAZ0SEiIxWIRJi9duiSuv2rVKnHltLQ0YTIxMVGYycnJEdc8fPiw\nMNm/f39hZuvWrTzPGwwG4aGHh0dFRYX406qqqsQji6ysLHF+xowZ9FsJCQlibfxvnwMnTpwQ\n52/duuXt7S3ML1myxFm/PXADj3oKoDmdC28SOsTPz2/cuHFNLoqOjhaPCHQ6nTgvvqxrNC94\n8sknY2NjhfGePXuIqKSkJDc3l4g8PT3Hjh1LROfPnxdWsFqtgYGB4psqOp3ObDYLi8R1iOij\njz6KiYkRH2q12k2bNom12YqKinriiSfEh2FhYUOGDBHG+fn5j/olQHvW6CmA5nQuBLRDQkND\nH7VIfO3WiEqlav5niofVu3fvJqL9+/fzPE9EqampQqBfvXq1xcLKy8vFsa+v7/Tp08WHf/jD\nH8QXoY2Eh4c3momIiBAGJSUlLe4U2qFGTwE0p3OpW14FHu1RKeyItLS0JUuWENH58+cLCwvF\nt1wmTJggDKKiooRBQECAcJT9ML1eL47v3LmzcuVK8eGuXbt+/vnnJ5988uGtbt269agZ2wN/\nAFGjpwCa07kQ0Mzp3r17//79T506RUQ7d+78/vvviahDhw7PPvussIJ4tWlVVVW/fv18fHzE\nbUtLS4XPxYiX5RHRrFmzbt++LT60WCyTJk06efKkp6dno11fu3bt9OnTffv2FR6WlZWJ1652\n797dqf+X4J7QnM6FUxwsEs9yrFy5sqysjIjGjBkj9nqPHj0ee+wxIrJare+884641ebNm0ND\nQzt16hQeHi6+0ty5c2dWVpb404TrTM+dO7d48eKH98vz/KRJk65fv05EVVVVr7zyyt27d4nI\n29t7/Pjxrvl/BbeC5nQymd+kVCbbq/QbLRKv4hg4cKA4KYSs4LvvvhPnp06dKkyKV3EIioqK\nGr1P8u2339qu8Pe//11c1K9fv0mTJg0cOFDcZMqUKcJq5eXl4oXVQ4YMsS1PrVaL74k3utTU\nw8Oja9euth80mDt3rvN+eeAOmnkKoDmdCAFtD1cHNM/zKSkp4iY6ne7+/fuNVliwYEGT7ze+\n/PLLZrNZWOfll18W548dOyZU4u/vL8z07dvXZDLxNs+BIUOGJCQkNPqBL7zwQk1NjZN+c+Am\nmnkK8GhO58EpDkaJZzmI6LnnnvPy8mq0wpIlS44cOZKenh4fH+/t7d21a9fnn3/+yJEjW7du\nFZ4be/fu/eKLL4SVx48fL1yTFBwcPHfuXGHy9OnTH374oe3P1Gq1Bw4cmDlzpl6v9/T07Nmz\n5yeffPLVV181+WFIgEdBczoLx/O83DVAE8rLyzt27Cj86+zduzc1NdV1+5oyZcrGjRuJKCUl\n5dChQ67bEUBbtfPmxBE0o6qrq4V0DgoKsr2DHQC0H7jMjjmVlZWVlZXi6ennn39eo9HIWxIA\nyAIBzZzOnTsbjUbxYWZmpozFAICMENDsUqlUS5cuHTBggKt3NGDAAOFPQq9evVy9L4A2aefN\niTcJmfPZZ59VVlbq9fphw4ZFR0fLXQ4AyAYBDQDAKFzFAQDAKAQ0AACjENAAAIxCQAMAMAoB\nDQDAKAQ0AACjENAAAIxCQAMAMAoBDQDAKAQ0AACjENAAAIxCQAMAMAoBDQDAKAQ0AACjENAA\nAIxCQAMAMAoBDQDAKAQ0AACjENAAAIxCQAMAMAoBDQDAKAQ0AACjENAAAIxCQAMAMAoBDQDA\nKLXcBdipqqqqurraw8MjLCzMwwN/ZkDZ0M/QJIW1gsFgmDhxol6v9/f3j4yMDA8P12q1kZGR\naWlpx44dk7s6gLZBP0PzOJ7n5a6htWbNmrVmzRqe5/V6fXR0dHBwMBGVl5cXFxcXFxcT0eTJ\nkzds2CB3mQCtgn6GlvEKsWbNGiIaNWrUyZMnH15qMBgmTJhARCtXrpS+NoC2Qj9DayjmCHro\n0KF37twxGAxqddPnzXmeT05OtlqtR48elbg2gLZCP0NrKOYctMFgGDx48KO6mYg4jktKSjIY\nDFJWBWAf9DO0hmICOj4+Picnx2KxNLPO8ePH4+PjJSsJwG7oZ2gNxQR0enr6+fPnx4wZk5eX\n9/DS/Pz89PT0Q4cOjR07VvraANoK/QytoZhz0EQ0bdq09evXE1FUVFRMTExQUBDHcRUVFUVF\nRZcvXyaijIyMTZs2cRwnd6UALUM/Q4uUFNBElJubu2zZsgMHDpSVlQkzKpUqNDQ0JSUlMzMz\nOTlZ3vIA2gT9DM1TWECLjEZjdXW1RqMJDQ3FJ69A6dDP0CSlBrQszGY6fJiio6lrV7lLAXAY\n+pl9CGiqrq42m83Nr6NSqXQ6XWoq7dtHKhXt3UujRklTHUDboJ/difsEtNFoHD58OBGdOnWq\n9VsVFhZ27dq1xV8Cx3ElJabQ0IarVv/0J/riC7srBWgZ+hlIuXeze5jFYsnNzW3rVrGxsXl5\nebW1tc2sc+bMmVdffdXb28pxJHT+zZt2lwnQKuhnIHcKaJ1O98MPP9ixYa9evZpfoa6ujoi0\nWtLpqLKSiKi01I79ALQB+hnInQJao9E8/fTTLt1FSAgaGiSCfgZS0CcJRbdv375w4UKTb4OU\nlZVdv37ddbsOCWkYlJaSu5y6B5mhn6EZSgro3Nzcvn37hoWFde/ePSoqasuWLY1WePnllyMj\nI11XQGhow8BspooK1+0H2gX0M7RIMac4CgsLn3rqKZPJNGLECK1We/DgwYyMjJqamunTp0tW\ng9jQRHT7NgUFSbZncDfoZ2gNxRxBL1iwoK6ubs+ePQcOHNi7d++1a9e6dOny9ttvX7hwQbIa\nGjU0gN3Qz9AaignonJyckSNHPvPMM8LDkJCQvXv3chw3Z84cyWpAQ4OzoJ+hNRQT0GVlZVFR\nUbYzcXFxs2fP3r17908//SRNDbYNXVIizT7BPaGfoTUUE9B9+/bNzs5uNDl37tyoqKhp06aZ\nTCYJaggLezDGEQc4Av0MraGYgE5KSjp37tysWbOEy+wFPj4+69evP3v27MSJE5v/9JRT4IgD\nnAX9DK0i05fVttn9+/eTkpKIyM/P79lnn7VdtHDhQiKKiIgICQlxxf/RsWPHiKiurq60lCdq\n+O+555y+H2hH0M/QGoo5gvby8tq1a9e8efMiIiIuXbpku2jx4sWbN2/29fUtdfEnooKDSaNp\nGOOIAxyBfobWcJ+72fE8f/Xq1cLCQqd/QDY7O3vo0KF1dXVarTYigm7cICJ6/HEqLHTufgAe\nQD8DKeiDKi3iOK5z586dO3d26V46dWpo6Fu3XLofaO/Qz0AKepOQEZ06NQzu3aOqKllLAXBY\nhw4NTXzvHm3d+o/i4mJ564FGENBtY3tlEg46QOkMhn+J49dem79o0SL5aoEmIKDbRjyCJgQ0\nKJ9K9eB9yMGDn7NYLDIWAw9DQLcNAhrciW1A19YGyFgJNAkB3TZ6/YOx8O4KgHKp1bYBjdvZ\nMQcB3Ta2AY1vcgOlsw3oujoENHMQ0G0THv5gjIAGpVOrH9yDo7Y2UMZKoEkI6LaxWh98BdGF\nC1UV+CIKULLfnuJAQDMHAd0248c/Q2QUxj//XDxv3jx56wFwBMfVenk13JUJ56AZhIBuG5PJ\nFBJSL4w1mhhpbgsJ4Dp+ftXCAAHNIAR0m4kNXV/vY7Fo5S0GwEHoZ5YhoNvMz+/BR7zv3cOl\no6Bs6GeWIaDbTDziIKJ79/C+Cigb+pllCOg2sz3iqKnBEQcoG/qZZQjoNvvtS0IccYCyoZ9Z\nhoBuM50OLwnBfaCfWeY+N+y3T1FR0ejRo5v/gk5hqfjVMzqd7REHrkwChqCf3Ux7D+iwsLA5\nc+Y0fzlzYWHhsmXLOI4THvr43FWrebOZI6KaGhxxAEPQz26mvQe0VqvNyMhofp3s7Oxly5aJ\nDzmODwkx37ypIaKaGhxxAEPQz24G56Dt0alTw4cJ79/3N5vlrQXAUehnZiGg7REW1tDQPO+B\nu0KD0qGfmYWAtod4xEFERUUyFgLgBOhnZiGg7WHb0NeuyVgIgBOgn5mFgLaHXo+GBveBfmYW\nAtoetg2Nl4SgdOhnZiGg7dGp04PrTK9elbEQACdAPzMLAW2PwECLt7dVGKOhQenQz8xCQNsp\nIqLhVSEaGtwA+plNCGg76fUNrwqrqgjfHAtKh35mEwLaTuIRBxFduSJfHQDOgH5mEwLaTuHh\nD95XuXxZxkIAnAD9zCYEtJ0iIh40NI44QOnQz2xCQNvJ9iXhpUsyFgLgBOhnNiGg7RQZiZeE\n4D7Qz2xCQNvJ39+i0dQIYxxxgNKhn9mk1ICuqqq6fv36zZs3rVarXDV06FAiDC5fJvmqAHeA\nfoYmKSygDQbDxIkT9Xq9v79/ZGRkeHi4VquNjIxMS0s7duyYxMX4+NwSBnV1dP26xDsHd4B+\nhuYpKaBnzZrVp0+frVu3chyXkJCQmpqampo6aNAgjuOysrISExOnTJkiZT0+PjfFcWGhlHsG\nd4B+hhYp5jsJ165du3r16lGjRi1durR///6Nlp49e3bJkiUbN27s0aPHW2+9JU1J4hEHERUU\nUEqKNLsFd4B+htZQzBH0tm3bunXrtmfPnoe7mYh69eqVlZWVlJS0Y8cOyUqyPeK4eFGy3YI7\nQD9DaygmoA0Gw+DBg9XqRx7ycxyXlJRkMBgkK+nu3VxxvG1bzocffijZrkHpGOxn24AuKJBs\nt9AcxQR0fHx8Tk6OxWJpZp3jx4/Hx8dLVlJFhYHj7gvj8vKOW7dulWzXoHQM9rOX1x21uuFq\n6F9/tZhMpubXBwkoJqDT09PPnz8/ZsyYvLy8h5fm5+enp6cfOnRo7NixEhbF63QNVybV18co\n6JcJsmOwnw2GPLP5V2H866/1w4alSLZreBTFvEk4ffr0vLy89evX79u3LyoqKiYmJigoiOO4\nioqKoqKiy5cvE1FGRsbs2bOlrMrH53plZWciMpvV9fV6KXcNisZgP5vN5pCQitJS4ZFXaam3\nZLuGR1FMQBPRunXrMjMzly1bduDAgaNHjwqTKpUqNDT0pZdeyszMTE5OlrgkP78H14uaTI9J\nvHdQNAb7OSjo9n8DGv3MBCUFNBH169dv+/btRGQ0GqurqzUaTWhoqIeHbOcWfH1tA/pxucoA\nhUI/Q/MUFtCigICAgIAAuasgX99icYyGBruhn6FJeF/LIb6+1zmuYWwyxcpaC4Cj0M+sUeoR\n9MOMRuPw4cOJ6NSpU63fqqKiYsGCBWazuZl1SkpKHrVIra4NC6u/dUtDRHV1OOIAp0E/A7lT\nQFssltzc3JbXc7bY2DqhoS2W4LIy6thR+hLADaGfgdwpoHU63Q8//NDWrQIDA9esWdP8OtnZ\n2Tt37nzU0tjY2mPHfIXxuXM0bFhbSwBoAvoZyJ0CWqPRPP3009LvNza2ThwbDGhocA70MxDe\nJHRcly6/aWgARUM/MwUB7ajY2Frxje+mPrULoCToZ6YgoB3l42MVv7LeYCCel7ccAIegn5mC\ngHaCuLhaYWA00rVr8tYC4Cj0MzuU8Sbh6tWrFy5c2MqVKyoqXFrMw+Liag8e1Anj3FyKiZF4\n/6Aw6GdoJWUE9OjRoy9evPjpp5/W1dX5+fnFMNYy3brViuPTp0nSO56CAqGfoZWUEdBdunRZ\ntWpVamrq6NGjk5OTd+/eLXdFv9Gjx4OGbsvHvqCdQj9DKynpHPSoUaPi4uLkrqIJ4eEmL6+G\nr1Y5eVLeWkAx0M/QIiUFNBENGjRIo9HIXUVjHEc6XcP31F+7RhwXqtPp7t27J29VwD5m+1mv\nb/iG72vXSLxDNEhPYQH95ZdfSvk9x63n63tBHL/22trq6ura2tpm1gcghvtZr78hjk+ckLGQ\n9k5hAc2sgIAHX4NcU9NTxkoAHBce/iCg//MfGQtp7xDQzuHvf1EcFxQEyVgJgOP0+gdfrfLz\nzzIW0t4hoJ2jQ4dbKlW5ML54MVDeYgAcFBhYIfYzAlpGCGin8fRsuHtvZaUnEb6NApTN2/uM\nMLh9mwoL5a2l/UJAO42np+0lo0/JVgeAw8xms0r14Nzz9u2XZSymPUNAO42np+0lo0NkqwPA\nYQaDobLyO/HhO+98V1VVJWM97RYC2mk8PXNVKvHeX4lylgLgGIvFEhNzy7afm/+eQ3ARBLTT\ncNw9m8/IxldUcM2tDcA29DMLENDONGBAzX+H3PHjzH1CDKBN0M+yQ0A7k01D09GjyrgRFcCj\noJ9lh4B2poED73l4NJy2O3oURxygbOhn2SGgncnPz9KzZ8Npu3PnVCUl8pYD4BD0s+wQ0E6W\nkHBXGPA8/fCDvLUAOAr9LC8EtJM99dRdcbx/v4yFADgB+lleCGgne+KJe15eDVeM7t9PVqu8\n5QA4BP0sLwS0k2k0fO/eDXc4v30bt2oEZUM/ywsB7XwDBtwSx3v2yFgIgBOgn2WEgHa+AQNu\nETVcnPSPf8hbC4Cj0M8yau8Xn5tMpu3bt5tMpmbWKWzjzRaDgu4T/UI0iIgMBsrPJya/GhTc\nEPrZzbT3gC4pKVm+fHnz3x8oLOV5vpl1HrJDaGgi+uYb+utf7a8QoPXQz26mvQd0VFTU2bNn\nm18nOzt76NChHNemm8V8Q7RUGH31FRoaJOKKfjabzbb9vHp16YwZWn9/f4cKhdbBOWjnq6qq\nIirw9j4nPDxzhnbuvCRvSQB2u379OlGBl1dD7t+8GbJt2xl5S2o/ENDOV1FRQUQJCQ9C+Ysv\n5KsGwBkmT/YRxwcPRshYSbuCgHaVN94IE280c/BgRH29vOUAOGTEiFL0s/QQ0K7SsaNp6NCG\nj8lWVHjiAlJQNPSzLBDQLjR+fIU4XrdOxkIAnAD9LD0EtAsNH14dGtpwH4MffqBff5W3HACH\noJ+lh4B2IZWK/5//KRfGPE//93/ylgPgEPSz9BDQrvXii+VEDZ8a2LqVbt6UtxwAh6CfJYaA\ndq3gYLNanSWMa2tp+XJ5ywFwCPpZYghol1OrPxGvT1q/nm7ckLccAIeoVB+L/bxuHX/1Ki64\ncyEEtMtxXEFKynVhfP8+LVokazUAjjGZzlqtDZ+8qq3lXnihhU+WgyMQ0C5nNpu12o88PCzC\nw7/9jc/NlbciAPvxPD9vnkmtbjiI/uWXPuhn10FAu1x9ff2VK/8KDf278NBq5f73f+WtCMAh\nUVGmCRPEyzk80M+ug4CWwqxZs775pndAgEXuQgCcY9q02+hnCSCgJeLvb/n442uennk+PtlV\nVTNefPHFF1988fPPP5e7LgB7CP3s4/Pr448XLl0qdzXuCwEtnUGDary8kqKjJ3focJvneYPB\nsG3bNrmLArDToEE1vXu/mpa2uXNnuUtxX0q9YX9VVVV1dbWHh0dYWJiHh5L+zAwbNmzmzJlE\ntHr16oKCArnLASYot5/BpRTWCgaDYeLEiXq93t/fPzIyMjw8XKvVRkZGpqWlHTt2TO7qANoG\n/QzNU9IR9KxZs9asWcPzvF6vT0hICA4OJqLy8vLi4uKsrKysrKzJkydv2LBB7jIBWsUN+vn6\n9et/+9vf9u3bJzwcN27c/Pnz5S3JzSgmoNeuXbt69epRo0YtXbq0f//+jZaePXt2yZIlGzdu\n7NGjx1tvvSVLhQCt5x79XFVV1b179yFDhhBRdnb2oUOHENDOpZiA3rZtW7du3fbs2aNWN1Fz\nr169srKybty4sWPHDpYb2lZ5eXlBQcG8efOEh507d546daq8JYFk3Kaf+/Xr9+qrrxJRVVVV\nXl7eiRMnhPng4ODOePfQYYoJaIPBMG7cuCa7WcBxXFJS0po1a6SsyhGFhYVGo/Hw4cNEZDQa\ni4qKENDth/v185kzZ/7zn/8MHDhQeBgUFHTnzh15S3IDigno+Pj4nJwci8WiUqketc7x48fj\n4+OlrMpBPXr0EE4y7t27d+HChZmZmcK8t7f3Bx984OPj0+zWoGDu188Wi2XgwIGrVq0iouzs\n7EW46YwzKOYqjvT09PPnz48ZMyYvL+/hpfn5+enp6YcOHRo7dqz0tTnu6tWrVqv1ypUrV65c\nuXjx4qpVqwoLC+UuClzILftZrVbrdDqdTtehQwe5a3ETijmCnj59el5e3vr16/ft2xcVFRUT\nExMUFMRxXEVFRVFR0eXLl4koIyNj9uzZcldqJ61Wu3LlSiKqrKxMTEyUuxxwLffuZ7PZbDab\nv/76ayKyWq2ff/65n58fx3FE5OHhMX/+/N69e8tdozIoJqCJaN26dZmZmcuWLTtw4MDRo0eF\nSZVKFRoa+tJLL2VmZiYnJ8tboRN98803//73v4lIrVaPGzcuMDBQ7orAydy4n/Pz800m0+TJ\nk4nIarXevXt35MiROp2OiP75z38mJCRERkYKawYEBAjBDU1SUkATUb9+/bZv305ERqOxurpa\no9GEhoa62Sev7t69S0SfffaZRqMholu3blmtVqHXwc24az9brVYvLy/hszZFRUWpqamZmZlx\ncXFEtHv37rfeeku8NGXEiBEvvPCCMI6Li0tJSZGpZEYpLKBFAQEBAQEBclfhElarlYjWrl0r\nNPSYMWMslobbhm3evNn29h39+/dftmyZLEWCc7lxPzditVqnTJkyYsQIInr99dePHz9+/vx5\nIqqpqQkODt6/f7+wmp+fX0hIiJyFskGpAd1+WK3WsrKyS5cuEdGePXtu3LgxatQoIjpz5syu\nXbuEgDaZTOvWrautbfg2zzNnzsTFxXl5eQkPx40bJ2Q9AAv0en3Pnj2JSKvVjhgx4v333yei\nd999d8eOHbGxscI6Go3m5MmTwpuNlZWV/v7+4uZRUVHCi8v2wH0C2mg0Dh8+nIhOnTrVpg3P\nnj0rRluTLly4YPvw5s2b586dIyKTyWQ0GoVxZWWlyWQSxkVFRcJWvr6+wibXrl0TFlksltLS\nUmF87969+vp6YVxaWmq1WoVxSUkJERUWFprNZmF3CxYsWLBggfCjkpOTBw8eTEQFBQVXr14V\nLju9f/++sG2TLl68OG3aNKHguro6Pz8/IuJ5vry8XPh4Mc/zO3fuFKutrq4eMmRIWFiYUCQR\nCc8Ti8VSXV0tHOiFhIRER0e3/pcMbeWu/czzfJN7vH37dmho6Ny5c4no3LlzmzZtetQbiTNm\nzJg0aRK1k37m3UVZWZkd/0cFBQWteY+C47j6+nqe5xMSElz8D6IMmZmZrvlnhAboZykx288c\nz/Ny/3Kco76+/siRI0T09NNPt2nD6upq4W97M1QqlfAetMlkqqmpESaFk8XiWzr19fXiK69H\njc1ms0qlEp5CPM9bLBbxs2St2ZydPXp6euJaV5dCP6Ofich9AhoAwM0o9Rw0bnAO7gT9DE1S\nWCvgBufgTtDP0DwlneKwvcF5dHS07Q3Oi4uLiUiCG5wHBgYajUaX7oJlAQEBFRUVclfhJtDP\nsmO/nxVzioORG5wHBwdPnz59/Pjx9m0+ffr03r17Cxe92eG9994jonfffde+zdetW5eXl7d2\n7Vr7Nt+xY8dXX31l37bQCPqZ0M+toJiAZuQG52q1Ojo6esCAAfZtrtPp9Hq93ZsLB1l2b67X\n669evWr35r/88ksz9y+GNkE/E/q5FRRzDtpgMAwePLjFG5wbDAYpqwKwD/oZWnrsZGEAAAZ4\nSURBVEMxAS3e4LyZdZR1g3Noz9DP0BqKCWi3vME5tFvoZ2gN1k/BiNz7BufQ3qCfoTUUE9Dk\n1jc4h3YI/QwtUlJAk/ve4BzaJ/QzNE9hAS1qPzc4h/YA/QxNwt9qAABGIaABABil1FMcctFq\ntVqt1pHNHfm2Hkd2TUQajcbB4h0sAFiDfnakAAko6WZJLCguLg4NDbX737WkpMTX19fHx8e+\nzYUbuwQGBtq3eU1Nzd27d4Xv/rGDyWS6fft2ZGSkfZsDg9DPjPczAhoAgFE4Bw0AwCgENAAA\noxDQAACMQkADADAKAQ0AwCgENAAAoxDQAACMQkADADAKAQ0AwCgENAAAoxDQAACMQkADADAK\nAQ0AwCgENAAAoxDQ0DZ3797dsmVLcXGx3IUAOAHj/YyAbq1169YlJiYGBAQkJiauW7dO4r3X\n1dXNnz9/2LBh/v7+sbGxaWlphYWFEtcgmDVrVkZGxunTp2XZOzgL+lnAej/z0ApTp04lom7d\nur3yyitxcXFENHPmTMn2bjQak5KSiKhnz56TJ08eOXIkx3He3t6nTp2SrAbB119/LbTNnj17\nJN41OBH6WcB+PyOgW3bq1CkiGj16dH19Pc/z9fX1Qkvl5eVJU8Bf/vIXIpoxY4Y4s3fvXg8P\nj759+0pTgKC4uDgoKMjX15flhoYWoZ8FiuhnBHTLXnrpJSI6ffq0OHPixAkieuWVV6QpoHv3\n7n5+frW1tbaTI0aMIKKSkhJparBarb/73e8ee+yxv/71ryw3NLQI/cwrp59xDrplBw4ciIyM\n7NOnjzjzxBNP6PX677//XpoCPDw8kpOTPT09bSeFL/oUvnZTAitXrvzxxx+3bt2q0+mk2SO4\nCPqZlNPPCOgWGI3GsrKymJiYRvPR0dG3bt2qrq6WoIazZ8/u3r3bdqa0tPTgwYNhYWGxsbES\nFJCbmzt//vy5c+cmJiZKsDtwHfQzKaqfEdAtEFo2ODi40bwwU1VVJX1J+fn5Q4YMqa2t/eij\nj9Rqtat3d//+/fT09J49ey5atMjV+wJXQz8rq59d/utQOo1GQ0QcxzW51MND0r9wNTU1y5Yt\nW758Oc/zq1evzsjIkGCnc+bMuXTp0i+//CK8CAVFQz8rq58R0C0IDQ1VqVQPnxorLy9XqVRh\nYWGSVbJv376pU6deu3bt2WefXbFiRbdu3STY6b/+9a81a9Z88sknvXr1kmB34GroZ4X1s9zv\nUiqAXq9//PHHG01GRUVFRERIVsM777xDRL169Tp8+LBkO+V5fsWKFc00z8aNG6UsBpwC/ayg\nfsYRdMtSUlKysrLy8/OFS/qJ6OzZs0VFRcLlShLYsmXL4sWL//jHP27ZskXi12V9+/YVPtQg\nOnXqVE5OzjPPPBMTE9O9e3cpiwGnQD/bzrDez3L/hVCAH3/8kYj+9Kc/CQ+tVuuECROI6Kef\nfpJg71artVu3bhEREffv35dgdy366KOPiOHrRqFF6GdbjPczjqBblpycnJGRsXnz5hs3bgwe\nPPjo0aNHjhx57bXXpLlG5+rVqxcuXAgJCRk3btzDS7/44ouOHTtKUAa4DfSzgiCgW2XTpk09\nevTYuXPn6tWr4+Pjly9fPnv2bGl2fenSJSIqLS397rvvHl5aV1cnTRngTtDPSsHxPC93DQAA\n0AR8UAUAgFEIaAAARiGgAQAYhYAGAGAUAhoAgFEIaAAARiGgAQAYhYAGAGAUAhoAgFEIaAAA\nRiGgAQAYhYAGAGAUAhoAgFEIaAAARiGgAQAYhYAGAGAUAhoAgFEIaAAARiGgAQAYhYAGAGAU\nAhoAgFEIaAAARiGgAQAYhYAGAGAUAhoAgFEIaAAARiGgAQAYhYAGAGAUAhoAgFEIaAAARiGg\nAQAYhYAGAGAUAhoAgFEIaAAARiGgAQAYhYAGAGAUAhoAgFEIaAAARiGgAQAYhYAGAGAUAhoA\ngFEIaAAARiGgAQAYhYAGAGAUAhoAgFEIaAAARiGgAQAYhYAGAGAUAhoAgFEIaAAARiGgAQAY\nhYAGAGAUAhoAgFEIaAAARiGgAQAYhYAGAGAUAhoAgFEIaAAARiGgAQAYhYAGAGAUAhoAgFEI\naAAARiGgAQAYhYAGAGAUAhoAgFEIaAAARiGgAQAYhYAGAGAUAhoAgFEIaAAARiGgAQAYhYAG\nAGAUAhoAgFEIaAAARiGgAQAYhYAGAGAUAhoAgFEIaAAARv0/E1pjCx/tSq8AAAAASUVORK5C\nYII=",
      "text/plain": [
       "Plot with title “rexp”"
      ]
     },
     "metadata": {
      "image/png": {
       "height": 450,
       "width": 600
      }
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "n = 1000\n",
    "lambda = 2\n",
    "\n",
    "par(mfrow = c(1, 2))\n",
    "ylim <- c(0, 2)\n",
    "xlim <- c(0, 4)\n",
    "hist(rmyexp(n, lambda), breaks = 20, freq = FALSE,\n",
    "     xlim = xlim, ylim = ylim, xlab=\"\", ylab=\"\", main=\"rmyexp\")\n",
    "xax <- seq(0, max(x), 0.01)\n",
    "xDens <- lambda*exp(-lambda*xax)\n",
    "lines(xax, xDens, type = \"l\", col = \"blue\", lwd = 3)\n",
    "\n",
    "hist(rexp(n, rate = lambda), breaks = 20, freq = FALSE,\n",
    "     xlim = xlim, ylim = ylim, xlab=\"\", ylab=\"\", main=\"rexp\")\n",
    "lines(xax, xDens, type = \"l\", col = \"blue\", lwd = 3)"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "e01ebe0f",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "## Indirect Methods\n",
    "\n",
    "Indirect simulation\n",
    "\n",
    "-   What if the cumulative distribution function is difficult to invert,\n",
    "    or not even available?\n",
    "\n",
    "-   How to invert the CDF of a standard normal distribution?\n",
    "\n",
    "    $$F(x)=\\int_{-\\infty}^{x}(2\\pi)^{-1/2}e^{-x^2/2}dx$$\n",
    "\n",
    "\n",
    "-   It is still possible to simulate from this type of distribution?\n",
    "\n",
    "-   If the **density** is available, then the answer is YES!"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "5cac5f45",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "The mixture of normal distribution\n",
    "\n",
    "-   The mixture of normal distribution has density function\n",
    "\n",
    "    $$f(x, \\omega, \\mu_1, \\mu_2, \\sigma_1, \\sigma_2) = \\omega N(x, \\mu_1, \\sigma_1) + (1- \\omega)  N(x, \\mu_2, \\sigma_2)$$\n",
    "\n",
    "    where $0 < \\omega <1$ is the weight.\n",
    "\n",
    "-   It is based on the combination of the normal but has many features.\n",
    "\n",
    "-   It is not so easy to simulate from this distribution using the\n",
    "    direct method."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 6,
   "id": "87953753",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeAAAAFoCAIAAAAAVb93AAAACXBIWXMAABJ0AAASdAHeZh94\nAAAgAElEQVR4nO3dd1gU59oG8HthWZAuIB3FglhAsYKICrEh9tg1xm6MPZZ80RNbTIzHltjx\nqLFFMTHWoKiJJSoiNkRQEbCgoKBIFSnL7nx/zGayobnI7s4sPL8rV651ZnbmmS33vsy8846I\nYRgQQggRHj2+CyCEEFI2CmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhC\nCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhC\nCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhC\nCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhC\nCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmh12rNnj+hvkyZNKr1AQEAAO9fNzU375VXd\ntm3b2PrNzMw+bA1paWmi8hkbG3t5eS1YsODdu3fqqvnMmTPc+t+8eVPZp2/evFm5Qj09vczM\nzBLL1KlTR3mZcePGsdOr/nLpnLy8vPLeXAcHh44dOy5fvrzEm1sDXyXVUUBryk8//XT37l2+\nq9Ax+fn50dHRK1eu9PHxkUqlfJdTBoZhIiMjlac8fvw4PT1d7RuSy+V9/3b58mW1r1/7UlNT\nr169unjxYnd396SkJL7L0Q0U0Joil8vnzJnDdxW6KiYm5scff+S7irJdu3ZN+Z/Xr1/XxFYY\nhgn924sXLzSxCb4kJycPGzZMJpPxXYgOoIDWoHPnzoWGhvJdhXAtXLiw+G9SqfTNmzdbtmzh\n5p44cYLH2ioQERGh/M8SDWplkydPZvcuKytL83UJzsyZM7n3Nz8//969e3379mVnRUZGRkVF\n8VueTqCA1qx58+YVFxfzsmm5XM7LdlWnp6en/zexWGxlZfX555936dKFnXvv3j1+yyutbt26\nACIjIxmG4SayAe3o6Kivr19ieZFIxO1gpTaUkJCg3E5PSEiIjIx8+/bth5fOB+X318jIqFmz\nZjt37uTm3rhxg8fadAUFtKawZzwePny4devW9y4slUrXrVvXv3//Bg0aWFhY+Pr6Tp48OSYm\npsRiy5YtUz7HePTo0VatWrm7uwP44osv2FmdOnW6e/dux44dxWKxoaGhp6fnrl27ABQWFn73\n3Xf+/v4WFhaNGjUaP378y5cvS9Swa9eugIAAV1dXIyOjunXrduzYccOGDarkQkJCwrK/PXz4\nUOUXqQz16tVjH4hEIuXp0dHREydObNOmjampaaNGjYYNG3b16tXST09MTBw6dGidOnVsbW0H\nDBhw7NixqhRTQocOHQBkZ2c/ePCAnSKVStmWYIcOHUoUjLJOf0VGRurr63PvFLfk7NmzuZNp\n27ZtW7hwoZ+fHzd30aJFPj4+7C/WpEmT2MUCAgKUt7Vz5052uoGBATexgg8MS8VXVY3vL8fK\nyqqCuZXaTZaK+6JjGKI+u3fv5l7Y77//nn1gZWWVkZHBLuDv789ObNSoEfesu3fvtmjRovRb\nY2BgsGTJErlczi25dOlS7uk///wzmwiurq4Mw8yePZud5eLiYmlpWWJVa9asKfFBB+Dk5JSV\nlcWuuaCgwMfHp8xPiKenZ25uLrtYcHAwO9HU1FR5x5WP5Bw7dqyClyg1NZVb8uuvvy69ABdb\nHTp04CauW7dOIpGUru3LL79Ufn0uXLhQ+ms/ZMgQ7nF6erpq7+Q/Nm3axD19/fr17IMdO3aw\nc2/evMlOWb16tVgsZh+PHTu2gpdr7ty53ApPnDjBMMzTp0+5vfP395fL5YMHDy69s9euXWMY\nZuLEidySynXu2LGDnS4Wi7mJFXxgVH9Vmcq8v8o/57Nnz+amFxcXx8fHDxgwgJ3l7Oycl5dX\nwatUqd2s1L7oFmpBa0pAQAD7cczIyFi+fHl5i+Xn5w8YMIDr71G3bt127doZGhoCkEqly5Yt\nUw59Tm5u7qxZsxilP7Q5z58/z8rKMjExMTY25ibOmzfvwoULAGxsbLiJKSkpGzZsYB8vXbqU\n+5u6SZMmXbp0sbOzY/8ZExOzevVq1Xf8g+Xk5Gzfvp3rsTB58mT2wdmzZ+fMmVNUVATA19d3\n3Lhx7dq1Y2etWrVq3bp17OP09PR+/fplZGSw/7S3tzc1NQVw6NAhdVXYvn179mAF91pxB6DZ\nxrUqli9f3qhRI/bxwoUL5XL5kiVL2L0zNjbesWOHSCQ6dOiQ8pGxgwcPMgzj7e39wZWX/sCo\n+KpWxY8//sj9WSAWixs3bsz+QePq6hoWFqb8+awiLewLb3j+gahelMP02rVr8fHx7B9iBgYG\n8fHxTFkt6K+//pqdoqent3PnTnbiixcv2rZty063sbHhGuBcgwiARCL5/PPPt2/ffuDAAUap\nBQ1g0aJFMpksLy9v+vTp3MS6devGxcUxDHP37l02uQAMHDiQXXPTpk2553K706tXL3ZiYGAg\nO0W9LegKTJ06lV2+uLi4WbNm7ETlFjf3upmamr5584ZhmC+++IKdYmJiwrZMpVLp//3f/ymv\ntoot6NjYWC8vLwDNmzdn544ZM4Z9f9+9e6diC5phmL/++os7HjJ//nw9PUU7ad26ddwypQOa\n9WEtaPz7A6P6q8r6sBZ0eRYvXqzcqq1iC7qy+6JbKKDVqURAM0qpMWDAAKasgG7SpAk7ZeTI\nkcqriomJ4b7DR44cYScqf9+4iSwuoOvUqSOTydiJjx8/5pZfv349t/DIkSPZiX5+fgzDyOXy\ng397/fo1u0xOTk7nzp3Zxdq2bctOLC9xVKdKQCt/zWJjY9mJ7BUi3PScnBwuEENCQhiG4Y7z\nLl68WHmLrVq14tZc9YCeOnUqAJFIxB4dYt8+9vVRPaAZhpk2bVqJvfb29ubeOEYDAa38gVH9\nVa0sFc9kjh49mntKFQNac/siBHSIQ7MWL15sbW0N4NixY+xBBmVFRUWJiYns448//lh5loeH\nB3e1IXdKimNmZjZw4MAyt1i3bl2uRWZubs5N5/6sLjEdgEgkGjZs2KBBg5ydnbdu3Tp06FAv\nL686depcunRJtb1Us2+//ZZr+8fFxbEP5HJ57dq1uT+Zzc3NuQiLi4tLSUnJzc1l/1nilRwx\nYoQaa2MPZTAMc/369ezsbPaMmerHNzgrV67kTocCkEgkP/30E/fGqV2JD4yKr2oVN6rczU4q\nlSYnJ//3v/9lZ+3bt++nn36q4vpZ2tkXvlBAa5alpeWSJUvYx3Pnzi3ROT8lJYX7DDk5OZV4\nrrOzM/tAuSHMsrW1LW+LpfsSsCru6XXnzp2WLVv6+fktXrz4t99+y8vLGzBgAHeIQ0OUW8oy\nmezRo0c9evRgZ23evJnNPlUuOcvIyFDuWlDilaxfv74aa/b19WUfRERE3Lhxg2EYAOWdX62A\nqakp2xhn9e7dm/s7XRNKfGBUfFWruNES3SidnJy+/PLL/v37s3O5hnMVaWdf+CLmu4Dq7/PP\nP9+yZUtcXFxUVFSJvkFOTk5isZjN6NJXi6WkpLAPXFxcSswqL4U/TGFh4aBBg9ifgeHDh//4\n44/sGcKFCxeGhYWpcUMV0NPTa9CgwTfffHP27Fl2yr1799zd3bl9t7S0LO+qHwcHB+WLrV++\nfKl8LpRrWatFgwYN7Ozs0tLSrl27xv3mfUAL+s2bN2vXruX+eeLEievXr7dv3171NTBlnSIu\nT4kPjIqvqurrV12zZs2OHz8OID4+XpXl37ubPO6LFlBAa5xYLF6zZk2fPn0AlBhfQiKRNGzY\nkG39HT16VPlv8/v37yckJLCPmzdvrtEKo6OjuUb6N998o9x/Q6PbLY3bNAB2TCKu025OTo6X\nl5eJiQm3wOvXr9mLcczMzGrXrs1NP3r0qKenJ/fPkydPqrfIDh06HDt2jAtoW1vbD2ikz5gx\n49WrV9w/ZTLZuHHjbt++zXbgqQD3q1Bi4KcSvdorpuKrqvoKVccdbSjd7FCm+m7yuC9aQIc4\ntKF3797dunUrcxYXygcOHNi7dy/7ODU1dezYsexny9LSkru4TkNycnK4x1zf/tDQUNWjTV0X\nMij/gOXl5QFo2rQpG39yuXzx4sXc3N27d9va2trb2zs6OiYlJdWuXZs7ZL969eozZ84AYBhm\nw4YNhw8fLr2h8PBwruDs7OxKFcke5cjMzGQb+x/QfD5+/HhISAj7eO3atWwH3vv373/zzTdl\nLs++FCzuyPW9e/fYpiiAc+fOKbfH30vFV5Wbrpb39/Xr1z/88AN36RDXE65Mqu9mZfdFx/Bz\nbrKaKt2Lg3P37l3lo8BcL468vDxXV1duesOGDX19fWvVqsVN2b59O7cS5esOSmya68XB9bhg\nGEb5D//Tp09z06dMmcJOZHtxpKamKp+eatmypaenp/IfxR4eHuwTNX2hivKfvatWrWInKies\nl5fXuHHj2rZtyxU8adKkErWxnJ2dlZvVLK4Xx8qVK7mJT58+raDgEr04GIYpMbbc999/zy6p\nYi+OjIwMe3t7drqvr6/yeycWi2/dusUtyV1wVK9evenTpz9+/JhhmPPnzytv3d7evsRulneh\nSon9UvFVZam3mx0AIyOj6OjoCl6lSu1mpfZFt1ALWks8PT0nTJhQerqxsfHRo0e5gxiPHj26\nevVqfn4+AAMDg6+//rrMZ6mXnZ3drFmzuH9GR0fHxMTUr1+f6/8QFxfHdWbSKOVrIJX7t3z9\n9dfsz9udO3d27dp18+ZN9s+L0aNHc1fSjx07VvlPjeTkZPYgCTdAj7q0bdtW+VxCZVvQs2bN\n4n6l2CuAvv76awsLCwDFxcXjx4/n/ozgTpkmJSVt2rSJPSQSEBDAnWcDkJqampmZaWJiotzn\nXRUqvqqaIBaLN2zYUObVs5xK7SaP+6JpFNDas3z58hL921heXl63b99etWpVnz59XF1dzczM\nvL29J0yYcPPmzeXLl6v3fGB51qxZw35nTExMWrduPWfOnKioqOHDh7Nzi4uLlYe50Zw6depw\n3ZZ37NjB/SosX7780qVLo0aN8vDwqFWrlpub26BBgy5durR3717u7xJDQ8OLFy8ePnx46NCh\n9evXt7Gx6dWr14EDB5Q7S6iFkZFR69at2cf6+vrcJUWqOHny5L59+9jHH3/8MXu0xNramrug\nJjo6esWKFezjzZs3jxkzxsHBoVatWk2aNOEOpB46dOj7779v1aqViYmJlZXVwIEDb9y4wV5B\nUymqvKpqZG1t3apVq3Hjxj148KDM21mUUKnd1PK+aI2Iqcy5YEKqkzVr1syfPz87O7vMH05C\neEctaFJzXblyxdramtKZCBYFNKmJkpOTZ82adfz4cbrrDREy6gdNaqL9+/f/+uuvq1atmjdv\nHt+1EFIuOgZNaqKcnBwzMzPtnIAl5INRQBNCiEDRMWhCCBEoCmhCCBEoCmhCCBEoCmhCCBEo\nCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEo\nCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEo\nCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEoCmhCCBEo\nCmhCCBEoCmhCCBEoMd8F6Ibo6Oji4mK+qyCEaIRYLG7ZsiXfVZRB5wP61atXycnJ7u7uJiYm\nGtrEzZs327Vrp6GVE0KE4MaNG23btuW7ipJ0KaCTkpKWLFni4+MzZcoUADdv3pw0adKdO3cA\n6Onp9e7de8uWLc7OzmrfblFREYDCwkKJRKL2lRNC+FVUVGRoaMh+zYVGZwI6MTHRx8fnzZs3\nXl5eABISEjp37lxQUNCjR48GDRo8ePDg999/v3nz5r1792rXrs13sYQQogY6E9ALFizIyMjY\nvn37hAkT2H8WFhaePXu2W7du7AK//PLL8OHDFy9evHHjRl4rJYQQ9RAxDMN3DSqxt7d3dXW9\ndu0a+08XFxdPT89Tp04pL9O9e/eXL1/Gxsaqd9NXr17t2LEjHeIgqrh2DYcO4flzmJqiWzcM\nHgz61Agce4gjPDzc19eX71pK0pkW9Lt37xo2bMj9s6ioyNHRscQy9evXv379unbrIkQhIwOT\nJuHIkX+m7NqFJUuwbx98fPgri+gynekH3bZt24sXL+bk5LD/bN++/Y0bN5Sb/3K5PCIigj1C\nTYiWpaSgQwdFOhsYoEULsKdCEhPh74/jx/mtjugqnQnopUuXpqen9+zZkz3KsXz58sePH//n\nP/+RyWQACgoKZs6cGRsbO2DAAL4rJTVOdjZ69EB8PAAMGoSkJERHIzUVa9dCIkFhIYYNw+XL\nfFdJdBGjO0JCQsRiMQAXF5dOnTo1aNAAgI2NTdu2bc3NzQGMHTtWE9sNDw8HUFhYqImVk2rg\n448ZgAGY6dMZufxfs8LCGImEARh7eyY1laf6SIUKCwsBhIeH811IGXSmBQ1g+PDhjx49mjNn\njkwmu3z58uPHjwGkp6fHxsb6+vqeOXNm165dfNdIapyfflIc2ejXD+vXQyT619zAQGzZAgCp\nqfjsMx7KIzpNZ3pxlPD27dusrCypVGpsbFynTh09PQ3+0lAvDlKe16/RpAkyMuDsjLt3UV4X\n/BEjcPAgABw5goEDtVkgeT8h9+LQpRa0MlNTU2dn5/r169vZ2Wk0nQmpwNdfIyMDALZsKTed\nAWzcCGtrAJg3D4WFWqqNVAMUbYR8oAcPsHMnAPTujb59K1rSxgbLlwPA48cIDtZGbaR60Jl+\n0O+VlZUVEBAAICoqSvVn5eXlrVmzJj8/v4JlkpKSqlocqY6WLoVMBn19rFr1/oUnTcL69Xj4\nECtXYvJk1Kql+fqI7qs+AS2TydiBkyolNzc3MjJSKpVWsExKSgposCTybw8e4LffAGDkSDRr\n9v7lxWIsWYKRI5Gaih07MGOGpgsk1YGuniQsTSqVXrp0CUDXrl3Vu+Zt27ZNmTIlNzfX1NRU\nvWsmumvcOOzeDX193LsHd3eVniKToVkzxMfD1RUJCRBXn9aRbqOThNpgYGDQtWtXtaczIaW9\nfIkDBwBg4EBV0xmAvj7mzgWAp09x9KimaiPVia4GdE5OTkpKysuXL+VyOd+1kBpn2zawowez\ngau60aNhYwMAGzaovypS/ehYQMfGxo4ZM8bBwcHCwsLZ2dnR0VEikTg7O48cOZK93o8QTZNK\nsW0bAHh7V3oUpFq1MHEiAFy5gpgY9ddGqhldCugZM2a0aNFi7969IpHI29s7KCgoKCioXbt2\nIpEoJCTEz89v0qRJfNdIqr9jx5CaCgBTp37I0z/7DGzH/f/9T51VkeqJ72vNVbV582YAPXv2\nvH37dum5sbGxw4YNA7B27Vq1bzo4OBhAbm6u2tdMdFH37gzAWFsz+fkfuIbAQAZgatf+8DUQ\nNaKxONRg//797u7uoaGhrVq1Kj23efPmISEhnTp1OqI8HC8h6paUhHPnAOCTT2Bk9IErmTAB\nADIzceyY2goj1ZLOBHRsbKyPj4+4/K5JIpGoU6dOar+dCiHKdu8Ge1qaDdkP06+f4lThnj3q\nqYpUVzoT0B4eHpGRkezoz+WJiIjw8PDQWkmkpmEY7NsHAG3bwtPzw9cjkWD4cAD44w/F4WxC\nyqQzAT1q1Ki4uLi+ffvGlHXyOz4+ftSoURcuXOjfv7/2ayM1xNWrePQIAD79tKqr+uQTAJDJ\n8MsvVV0VqcZ05mKmqVOnxsTEBAcHh4WFubi41KtXz8rKSiQSZWZmPn/+/MmTJwDGjh07b948\nvisl1db+/QBgYIBhw6q6Km9vNGqExESEhGDWrKqXRqonnWlBA9i6dWtUVNSIESPy8/OvXLly\n4sSJ48ePh4eHFxQUjBgx4uLFi7t27RKVGC+dEDWRSnHoEAB07w5bWzWskD3Kcf06njxRw9pI\ntaQzLWiWl5fXgQMHAGRlZeXm5hoYGNja2tJ40EQLzp1DejoAjBihnhUOG4ZvvwXD4NAhfPml\netZJqhldjTZLS0sXFxd7e3tKZ6Id7MHiWrWgrtMcHh6KYfDYhjkhpVG6EfJ+RUWKPstBQTAz\nU9tqBw8GgFu38PSp2tZJqhMKaELe7+xZZGUBwNCh6lztoEEAwDCg66tImSigCXm/w4cBwNgY\nvXurc7UtWsDNDQAFNCkbBTQh7yGV4sQJAAgMhImJmlfO3uQ7IgJpaWpeM6kGdKwXh9oVFBQE\nBwcXVnin5cjISK3VQwTo4kXFrbs//lj9Kx84EKtWQS7HiROg0RhJCTU9oDMyMn799dcidvT1\ncrx+/RoAU13uDUYqi737iUSCPn3Uv/L27WFvj9RUHD9OAU1KqukB7ejoePXq1YqXYe9JSJfA\n1EwMg+PHAeCjj2Bhof716+mhb19s345z55CXp/5DKESn0TFoQipy/TpevAD+PlisCf36AUBB\nAf74Q1ObIDqKApqQirDdn9l2roZ07QpjYwAIDdXUJoiOooAmpCLs8Y327eHgoKlN1KqFbt0A\nIDQUdA9koowCmpByxcfjwQMAaru8uzxs9+q0NNy8qdkNEd1CAU1Iudjuz9B8QPfpA/Yk9MmT\nmt0Q0S0U0ISU6/ffAcDNDU2banZDjo5g77VJAU2UUUATUrY3bxAeDvzdy0LTgoIA4PZtugkW\n+QcFNCFlCwsDewtMzfXfUMYGNMPg9GltbI7oBApoQsrGdnqzskLHjtrYXPv2sLYGgFOntLE5\nohMooAkpg1SqaMkGBkKslett9fXRsycA/PEHiou1sUUifBTQhJTh0iVkZwPQyPgb5enVCwCy\nshARob2NEiGjgCakDOzxDbEYgYHa22iPHmDv4BYWpr2NEiGjgCakDGxA+/mhdm3tbdTWFm3a\nAKDzhESBApqQkh48QGIioN3jGyy2wX7nDl6+1PamiQBRQBNSEne1iPYDmj0MzTA4c0bbmyYC\nRAFNSEns8Q03N7i7a3vTXGc7OspBQAFNSAmZmYoLCNV7f1gV6euje3cA+OMPxWUypCar6XdU\nKSoqOnDgQMW3vLp8+bLW6iGVJpMhJgY3byIuDk+eID0deXkAYGQEa2u4uKBJE7RqhTZtYGSk\nyvpOn1Z0Q9b+8Q1Wz544eBAZGbhxAz4+/NRABKKmB3RaWtqqVasqvmlsTk4O6J6EQvP2LU6c\nwNGj+PNPZGW9f3kjI3TqhAEDMHgwbG0rWJA9vmFujs6d1VRqJfXsCZFIcc03BXQNJ6LceS/2\nnoS5ubmmpqZ810KAu3excSNCQhQtZY6RERo0gK0tTE2hr4+3b/HqFZKSkJPzr8XEYvTpg+nT\n0bVr6XUXF8PODhkZGDIEv/6qyb2oUKtWuHMH3t64do23GmqOoqIiQ0PD8PBwX19fvmspqaa3\noIkuuX4dy5YhLAxcq8LKCr16oXt3+PjAzU1xmUcJz57h+nWcP4+TJ/HsGYqLcewYjh1D69ZY\nvBj9+kHpdsDh4cjIALQ1QFJ5evbEnTu4eRNv3ijOGZKaiU4SEl3w6BEGD4aPD06dAsNAXx8D\nByI0FKmp+PlnjBkDd/ey0xlA3boYPBhbtuDpU4SHY+JExa2zb9/GgAHo2FG5mcp2sNPX1+oF\nhKWxW5fJ6DayNR0FNBG2wkIsWwYPDxw+DIaBoSGmTUNiIo4cQe/eMDCoxKpEIvj6Yvt2PHuG\nb76BlRUARETA1xcTJrAtZ3aEfh8f1KmjiZ1Rla8vzMwA6mxX41FAEwG7cQOtW2PpUhQUQCTC\np58iIQGbNsHVtUqrtbLCokV4/BgLFsDICAyDn35Cs2aJW87GxQF8H98AIJHgo48A4MwZ0Emi\nmqw6BHRmZqacboZczchk+PZb+Pri/n0A8PJCRAT27IGLi9o2YWGBFStw/z53x9bfpynaq7wH\nNP6+pDA1FXfu8F0K4Y8uBXRBQcGmTZvGjx+/YsWKhIQEAMeOHXNycrKysrKwsBgwYMCLFy/4\nrpGoQ2oqunfHokUoLoahIVaswI0b8PbWyLbq10doKA4cgLX1CfQD0NDgWbPiuxrZVmWwY0OD\njnLUcIyOyMzMbNasGVe2nZ3drVu3DA0Nzc3NAwICPDw82IkZGRlq33RwcDCA3Nxcta+ZlOHK\nFcbBgQEYgGnWjLlzRzubzXiQKhYVA8xs/MDUqsXs26ed7VagaVMGYDp35ruO6o69DCI8PJzv\nQsqgMy3o77777v79+3PmzLl79+4ff/xhZmbWuXNnOzu7Bw8enD9/PiYmJiQkJC0t7bvvvuO7\nUlIFO3fio48UI7mNG4cbN9CypXa2fOqWXTGjD6Cv3knk52P0aMyfz+/V1mwjOiJCcesAUhPx\n/QuhqmbNmvn4+HD/PHnyJIAVK1YoL+Pv7+/l5aX2TVMLWhtkMmbuXEXD2dCQ+d//tLz9oUMZ\ngKldmyk6c56pU0dRSZ8+DH/v+5kziioOH+arhBpBt1vQe/bsySlxLRYfnjx54uXlxf2zZcuW\nABo1aqS8TNOmTePj47VdGam6ggIMG4a1awHAzg7nz2PSJG1uv7BQcai3Vy8Y9AjA9eto0QIA\nQkPh74/UVG0Ww+ncGcbGAN1gpQZ7f0CPHTvWzs5u0KBBhw4dys/P10JNZXJwcGBPDLKsrKym\nTJnSuHFj5WVevXplzH6iiQ7JykLPnvjtNwBo3hyRkdD6FbcXLiguCO/fHwDg6oorVxAUBAC3\nbqFjR8UA/tplZAR/fwA4fZo629VQ7w/ozZs3e3t7Hzt2bOjQoba2tqNHjz558qRUKtVCccra\ntWt36dKl39kLCYBatWpt3bq1pdIBykePHp06dap9+/ZaLoxUSVoaAgJw6RIA+PvjyhXUq6f9\nKo4fBwBDQ0XnNgAwM8Px44qG/OPH6NQJ0dHaL4ytJzkZMTHa3zgRABUPhbx8+bI1ilAAACAA\nSURBVHLTpk1dunTR09MDYGVlNWnSpPPnz8tkMo0eguE8evTI2NhYJBK1adPm999/V54VExMz\nc+ZMCwsLkUh04cIFtW+ajkFryvPnjLu74jjr4MFMQQEvVchkim4jQUFlzV68WFFh7drMtWta\nri0xUbHxlSu1vOUaRMjHoCt9kpBN6s6dO7NJ7eDgMGvWrGta+eAmJCR8/PHHdnZ2mzZtUp7O\nBqidnd2vv/6qie1SQGvEkydM/fqK+Jk4kSku5quQq1cVVZR7YnL9ekYkYgDGzIy5dEmrxTGK\nn7AuXbS82RqkWgU0wzB37txZunRp/fr1lVvijRs3/u2339ReX5lKNNsTExPDw8OLioo0tDkK\naPV7/JipV0+Ri7NnM3I5j7XMm8cAjJ4ek5pa/kI7dzL6+gzAmJgwFy9qrziGmTOHARixmMnM\n1OZmaxAhB7Sq/aCLi4svXLgwe/ZsV1dXLy+vpUuXFhQUTJky5ezZs7du3ZozZ86LFy+GDBly\n8+ZN9R19KZfev8cta9iwoa+vr0Glxs0hPHryBAEBSEoCgK++wg8/KA/4qX1HjwKAry/s7Mpf\naPx47N0LsRh5eejdW3HQXCvYw9DFxTh7VmvbJILx3gj/7bffRo8eXbt2bXb5hg0bzps37+rV\nq/J/t3pu374N4KuvvtLYbwlvqAWtTklJjKurou28cCHf1TB37ihq+eEHFZY+eJARixmAMTVl\nrlzReHEMwzBMYSFjZsYAzJgx2tlgjSPkFvT7B+wfPHgwgJYtW86aNWvgwIEt2P6hpTRs2NDG\nxsaav9HFs7KyAgICAERFRan+rOLi4tDQ0Io7pdy6dauqxRHWixfo2hVPnwLAggUQwGWfbO8+\nkQgDB6qw9LBhkMsxejTevkVQEP78E+3aabhASCTo3h1HjiAsDHJ5uaNek2rp/QG9Zs2agQMH\nNmjQoOLFzM3NX79+raaqPoRMJrtT+YG/UlJSpk2bVnH/bvYHlqGeqFX0+jW6dVN0KJ43DytW\n8F0Q8HdAt22rcu++ESMgk2HMGOTkIDAQFy6gnCaLGgUF4cgRvHqF69fpLoU1y/sDeu7cuVqo\no+rMzc3//PPPyj6rXr16KSkpFS/D3pNQxOtxUp3HXo3y4AEATJ+O1av5LggAYmPBDgA9eHBl\nnvbJJygowOTJyMhAjx64dAn/vmBK7YKCFLeRDQ2lgK5Zqs/fSwYGBl27du1a1p1ACc/evUOf\nPmAPPY0bhw0b+C5Igb0trEhUyYAGMHEifvgBANLS0L07nj9Xe23KHBzQpg3w9x3HSc2hqwGd\nk5OTkpLy8uVLGqpf6IqKMHgwwsMBYMgQbN/Ob58NZb/8AgDt2uF9B/DKMmsWvvkGAJ49Q48e\n0PDxPfYeAnfv4tkzjW6HCIuOBXRsbOyYMWMcHBwsLCycnZ0dHR0lEomzs/PIkSPD2QgggiKX\nY8wYxWA/PXvi55+hr893TQpRUWBH1ho69ENXsWgR5swBgLg4BAUhN1ddtZXGBjTD4MQJzW2E\nCI4uBfSMGTNatGixd+9ekUjk7e0dFBQUFBTUrl07kUgUEhLi5+c3SbtDoJH3mzkTBw8CgK8v\nDh+GRMJ3Qf9g69LTw7BhVVjLmjUYOxYAbt7EgAEoLFRHaWXw8kLdugAooGsYvvv5qWrz5s0A\nevbsefv27dJzY2Njhw0bBmDt2rVq3zT1g/5Ay5Yp+hh7eDAauNNNVchkjIuLmu5XIpUy/fsr\n9nTQIM1dsz5tGgMwEgmTlaWhLdRQQu4HrTMt6P3797u7u4eGhrZq1ar03ObNm4eEhHTq1OnI\nkSPar42UYds2LFkCAK6uOHMGf1/oJBCXLytO7I0YUeV1icU4eBBdugDA4cOYMaPKayxbv34A\nUFSEU6c0tAUiODoT0LGxsT4+PmJxuf0CRSJRp06dYmNjtVkVKdvRo5g2DQDq1MGZM3B05Lug\nkn7+GQAkEgwZoo7VGRnh+HHF3bm2blWcPFQ3f39YWgJ/D45KagKdCWgPD4/IyEhZhfeIi4iI\nYO8eS/h06RJGjoRMBjMznDql6T7CHyA/X3F9Sq9eUNulrxYWCAtTdAdZsgT/+5+a1vsPiURx\nC4GwMM0d6ybCojMBPWrUqLi4uL59+8aUNXR5fHz8qFGjLly40F9xSwzCk5gY9O+PggJIJPjt\nN7Rty3dBZTh2DFlZAPDpp2pdr4MDTp+GrS0ATJ2qGIRJrdjr0XNyUPlLsohOev+VhAIxderU\nmJiY4ODgsLAwFxeXevXqWVlZiUSizMzM58+fP3nyBMDYsWPnzZvHd6U1WFISAgORlQU9Pfz0\nE3r04Lugsu3eDQDW1ujTR92rdnPDyZMICMDbtxg5EmfOoHNnNa4+MBC1aiE/H0eOoHdvNa6Y\nCBXfZykrJyoqasSIETY2Nlz9+vr6Dg4OI0aMuKixUXqpF4dK0tOZJk0qMzQcP5KSGD09BmBm\nzNDYNk6fZiQSBmAsLZmYGPWum+0wYmPDSKXqXXHNJeReHDrTgmZ5eXkdOHAAQFZWVm5uroGB\nga2trR4N8MU7dpRkdmCL+fMxezbfBZVr926wF5+OH6+xbfTsiZ9+wujRyMpCYCDCw9V4o8VB\ng3D8ONLTcfEiunVT11qJQOlqtFlaWrq4uNjb21M6808qxZAhiIwEgNGj8d//8l1QuWQy7NwJ\nAG3bwstLk1saNQpr1gBASgp69kR6urpW3K8fDA0B4NAhda2SCBelG6kahsH48YqLuXv1ws6d\nwhlqo7SwMMVYFpMna35jc+aAPSPy8CF698bbt2pZq4WF4tj+kSMoLlbLKolwUUCTqpk7V9Gp\n2Nsbhw5B2Dce27IFAMzN1XF9iipWrVL0FLl+HYMHo6hILWtlBw9JT8e5c2pZHxEuCmhSBStX\nKkbdbNoUJ0/CxITvgiqSmIgzZwBg9GiYmmplkyIRduxQ9Lc4cwZjxkAdgy/26wcjI+Dv4URI\nNUYBTT7Ujh1YuBAAXFxw5oz6LvnQlI0bIZdDJFJc5KglBgb49Vf4+gLAwYOYObPqqzQ3V2T+\n0aMoKKj6+ohw6VgvDrWTy+WXLl0qrvBg3gP2PiBE2W+/YcoUMAysrXHmDFxc+C7oPbKzsWsX\nAHTvjqZNtbttY2OEhqJzZ8TGYvNmWFtj2bIqrnL4cBw+jOxsnDyJQYPUUiURopoe0ElJSUOH\nDq04oOmehCWdPYtRoyCTwdQUp05pPfA+xLZtiuGa2QGcta12bZw5Az8/PHmCb76BpSW++KIq\n6+vTBxYWyM7G/v0U0NUa3x2xdQBdqPIvV64wJiYMwBgaMn/+yXc1KikoYBwcGIDx9GTkcv7q\nSEhg7O0ZgBGJmJ07q7iy8eMVb8KbN2opruYS8oUqdAyaVMatW+jdG3l5ijE2deQOkLt24eVL\nAJg/n9dOgI0a4exZWFmBYTB5suKWiB+K7R5SWIiQEPVURwSIApqoLDYWgYHIzlYMtTFgAN8F\nqaSoCCtXAkD9+trqXVcBT0+cOgUzM8hk+OSTqtwfpXNn1K8PAHv2qK06IjQU0EQ1Dx+ie3ek\np0MkwubNGD2a74JUtWMHkpIAYMEClD+cuBZ5e+PECdSqBakUQ4fi9OkPW41IpGhE37gBGgW9\nuqKAJipISEDXrkhNBYA1azBlCt8FqerdO3z7LQA0aKC4d6Ag+PvjyBEYGqKwEB9//MEXnIwd\nC3akA/b6dVL9UECT90lMxEcfISUFAL77jqduEB9o3TrF0edlywR2kWNgIH79FQYGyM9Hv344\nf/4D1uHqqjgLsG8fdYiuniigSYUSExEQgORkAFi2THFlio548UIxcFOrVhg5ku9qSuvXDwcP\nwsAA796hb98Pa0dPnAgAb94o7hFDqhkKaFK+uDh06aJI5yVLsHgx3wVVzrx5ihGK1q6FQAc9\n/PhjhIT8k9HspeiVMWAA7OwAYOtW9VdHeCfMjy0RgJgY+PvjxQsAWLYMS5fyXE8lnT2r6H82\nZAgCAviupgKDBikyOj8f/ftXtl+HRIIJEwDg6lVERWmkQMIjCmhSlhs3EBCAtDQAWLFC59rO\nubn47DMAMDdXjOYkaIMG4dAhxTnDwYMrOwbSlCmK3ikbN2qkOsIjCmhSyvnz6NoVb95AJMIP\nP2DBAr4LqrRZs/D0KQCsWgUnJ56LUUn//jh2TNH3btQoBAer/lQXF0WX9JAQxU8qqTYooMm/\nHT6MoCDk5kJfH//7n5BvXlWeAwf+GRdJGwPzq0tgIMLCYG4OuRyff47ly1V/6qxZAFBQgM2b\nNVUd4QUFNFGyeTOGDUNhISQSHDig6CKgU6KjFaFcpw527xby3V3K0qULzp1DnToAsHgxpk6F\nTKbK8/z84O0NAFu2IC9PkxUS7aKAJgAAhsGXX2L6dMhkMDNDaKjivh06JSUFffsiLw/6+vj5\nZzg68l3QB2jbFpcvw9UVALZuxcCBKibu/PkA8OYNtm/XYHVEyyigCfDuHYYOxerVAGBvj4sX\n0b073zVV2qtX6NEDz58DwKpVihv36SR3d4SHo2VLAPj993/60lRo4EA0aQIAq1fTRSvVBwV0\njZeSgi5dFNc5NG2KiAi0bs13TZX2/Dn8/XH/PgDMmKFbVzuWxdERly+jZ08AuHkT3t64fbvi\nZ+jpKc7mvnhBjejqgwK6Zrt2De3a4eZNAOjaFVevKv641ikREfDxAXvfmwkTsH493wWpBXug\niR32JDkZfn7vHVd05Eg0bgwA33+Pd+80XyHRPAroGiw4GP7+irEqpk7F6dOwtOS7psopKsLy\n5ejSRXEM4IsvsH27rp0YrIBYjK1bsWEDxGLk52PkSMyZg/Lv/iMWY8kSAHj5Ej/+qL0yieaI\nmJp9JyeGYSIiIt5V2N4IDQ1dv359bm6uqZbuBa15eXn4/HPs2wcAEgk2bqxUf7SsLCQk4MkT\nJCfj+XO8fo2MDGRno7AQubmKADE2hqEhTE1hYYHatWFjAycn2NvDxQWurnByqmqMyuU4fBiL\nFuHhQwAwNMSPP+rQKHuVdO4chg3DmzcA4OeHgwfL690tl6NVK9y9CwsLxMfD1larZeqooqIi\nQ0PD8PBwX/bevkJS0wP68ePH7u7uFd+TkFV9AvruXQwfrjgi4OT0zz2ny/foEa5fx+3biI5G\nTIxi2NGqkEhQvz4aNoSbG9zc0KgRGjVC3brvH3COYRAdjePHsWcPnjxRTGzRAnv3Kk6qVVtP\nnmDwYMWRaLYLYVBQmQueOYPAQACYPBnbtmmxQp1FAa3btm3bNmXKlOoQ0AyDDRvw1VeK0/zd\numH//vJaWbGxOH8ef/2F8PCKrk8zMYGdHaytYWEBM7N/jYifn49375CZifR0pKcjP/891enr\nw9kZdevC2Rl16sDSEsbGill5eXjxAo8f484dZGb+85Q6dbBwIaZNE9hQohpSUIDZsxWhKxJh\nxgysXIlatUov2Ls3Tp2Cnh4iI9G2rbbL1DlCDmgh3GGCaMXz5xg/Hn/+Cfx9tHLhwhKDvGVm\n4swZhIXh7NkymskSCZo1Q4sWaNYMjRujYUPUrVuJo9bZ2UhOxrNnePoUT57g8WMkJiIh4Z/T\nWTIZkpIUdz95rzZtMGECPv0UJiaqFqDzjIwUpw0++ww5OdiwAX/+iT17Smfwjz/i3DkUFuKz\nzxAZKYz7yJAPQm9dDcAw2L4d8+cjJwcA6tfHzz8rH9Z48gTHjuH333H5cslTUI6O6NIFvr7w\n9kbLlpBIPrwKCwtYWKB585LTU1KQmIhHj/D4MZKS8OwZ0tLw6tW/Wsp6erC1Rb16aNEC7dqh\ne3dd7GyiJsOHw9sbn3yCq1dx/z46dMD8+Vi8GEZG3CJubvjySyxfjtu3sW4dvvySx3JJ1fB7\nU3GdEBwcDCA3N5fvQj7I/ftM584MwACMSMRMnszk5LBzHj5kvvuOad1aMZP7z8yMGTiQ2bKF\nefiQ39KZ7GwmI4OrlygpLmZWrGAMDRXvWePGzLlzyvPz85kmTRiAMTJiYmL4qlI3FBYWAggP\nD+e7kDJQQL+frgZ0bi7z5ZeMgYHiO1y3LnP6NMMwjx4xK1YwLVuWzOUGDZgvvmDOnWMKC/mu\nnKjo7l2mXbt/3sIRI5jkZG5mZCSjr88AjKcn8+4dj1UKnZADWlf7Qefk5KSkpLx8+VIul/Nd\ni/DIZNi5E40bY9UqSKXQ18fs2Sln7/1wv6e3Nxo2xMKFiI5WLOvhgSVLEB2NR4+wbh0++qhK\nxzGIVnl6IiIC69aBPX0dEgJ3dyxfzg7f0b49/vMfAIiJwfTpvNZJPhjfvxCVExMT8+mnn9rb\n23P16+vrOzk5jRgx4sqVKxraqI61oI8fZzw8uFbV63a9ti581qULo6f3r/ayhwezfDkTF8d3\ntUQtnj9nhgz55911dGSCg5miouJipksXxbRNm/guUqiE3ILWpYCePn26SCQC4ODg4O3tHRQU\nFBQU5OPj4+zszIb1xIkTNbFd3QhouZz5/XfuD95MWO6ymhPYIkUs/lcuN27MLFrE3LvHd7VE\nEy5cYFq1+ufNrl+f2bHj5bMiJycGYMRiJjSU7woFiQJaDTZv3gygZ8+et2/fLj03NjZ22LBh\nANauXav2TQs9oIuKmJ9/Zg8qZ8FiL0b3MThtKC5WzmUXF2bePObWLb5LJZomkzH79jH16yu/\n9ze+2G9cSw4wxsbMxYt8Vyg8FNBq4Ovr6+7uLpVKy1tALpd36tSpY8eOat+0cAM6NZX59lvG\nyekV6mzHxCCclKBQOZft7Jhp05jLlxm5nO9SiTYVFjLBwUzdutxH4XeTYWI9GcCYmpbo7kEE\nHdA6c5IwNjbWx8dHXH6fe5FI1KlTp9jYWG1WxQ+ZDKdOYciQeJeua77O6pJywAEvJ2H7KQQV\nQQLAxgaTJ+PPP5GSgk2b4OdXjcYPIqqQSPDZZ0hIwM6d7CjRffJ+2ScfpQ/Z27cI6ikL2V3I\nd4lEJTpzoYqHh0dkZKRMJtPX1y9vmYiICA8PD21WpVVyOSIi3h049lfIi9OZ3qfwfSIaKc+3\nt0f//hg8GP7+dPEYASQSjB+PsWMRFob164f/+Ys+I/sEPxcWS0aN04tac2rFCogDu1GvHSHT\nmRb0qFGj4uLi+vbtGxMTU3pufHz8qFGjLly40L9/f+3Xplnv3kmPnwofsPo7y9Uf+RVZbfk2\nKHP/Bszk0tnNDfPm4fJlpKQgOBjdulE6EyV6eujdG2fPIi5uyNy6YZYjrJDBQLT6XpBff+v7\nNp0xciRCQhRD5RGB0aXBkj7//HP2cLCLi0u9evWsrKxEIlFmZubz58+fPHkCYOzYsT/99JNI\n3X/P8zBYklSaeeFOZMjjiEvSK0+dr8nbv4Ox8nyJWN7Rl+nVR79vX8WNjghRiVT6aPflIf/X\nICrTFYAERbPx4wJ8b6mfi7Zt0bUr/P3RoQN0fVywyhDyYEm6FNAA7ty5s2rVqj/++CM9PZ2d\noq+vb2tr6+/v/9lnn3Xp0kUTG9VGQDNM+u1n0cefRl1+G3Xf8MZr10SmIYOSvzRNHbK6Bhl2\n71fro49q1DeIqFlhIZYslK75USyTiwDURuYMbJyKLXZIAwCxGC1bwscH7dujdWs0aVK9/yij\ngFa/rKys3NxcAwMDW1tbPT3NHqhRe0AXFxQ/u/biUcSr+Ntv4x4wD1LM72U7pzJ2pZfUg7yp\nVVqn9oWdhzn49zR0cFDL9gkBgNu3MXMmwsMV/5SIpL1xciSzvxfCTKB0K3EjIzRvDg8PNG2K\nJk3g5oaGDWFoyEvNmiDkgNbVH0ZLS0tLYd+fKf/Nu1fxWS/vZ756+i7lUcGLZPmzF+Jnb0yS\n3lonF9tLUReoW+YTHQzS2zm/bNMG3gMdfXpbW1hQKhONaN0aV67g99/x3XeIjEQRY3AUA45i\ngKF+cUezu53zwnykl1shyrbgFW7dwq1b/zxTJIKjI1xd4eoKZ2c4OcHJCXZ2sLWFvT3MzPjb\np+pGVwNaaJ5FpCwa9Tg5yzSjwDijyPSNzDIPJoAx4FjxE81Eb91Nkps5Znk0Z1r4W7Xs72pf\nzwaw0U7ZhPTti759ce0atm/H4cPIzkahTHw+q/V5KG7ublMrr7HkaYOiuLr5D+2RWgevbZlX\nFinZlimpZuEJhii0QPa/1mhoCGtrWFmhdm1YWipu5WBuDnNzGBvD2Bjm5hCLYWkJfX2YmwOA\nuTn09f/5JwBLS+ociuoU0FlZWQEBAQCioqIq9cR79+4VsHcYKcezZ8/eu5KtcxL2PvGvYAEx\niu31X9c1Tq9nlevqJG3optewlblbF0cnrzoAneYjPPPxgY8PNm/GuXMIC8OFC3jwAOzhz/R8\nk/T85ldRaiTvf7NElggMAMvCLNELBi/+Nbc2Mst+mkLO3w/Sy5ipp1dGWOvrq5TgIpGpoXTT\nDiOPwTr5LdPVY9ClvXnzxsbGBkCl9ujRo0dubm6qPCUvL8/Y2Li8uXePJM4YnyeHXu1aBdam\nhVYWMhsb2Dvq1XExsm9k6uhhZdfcRl9Sbg9uQoQmMxO3byMqCnFxSEjA06d4+RJSKd9lfZCv\nfC5+H+Ff3lwhH4OuPgEtlUovXboEoGvXrpV6Ym5ubsU3jb1+/XpgYGBhYaGEuvSTmi0tDenp\nePMGWVnIzsa7d8jKgkymuFdPXh6KihRLFhSUugulXI7iYhQXQy6HVAqGUfyf/fax05UfACV/\nEJRnlcCuqiy1jJhv9tWv51PuuRwhB3T1OcRhYGBQ2Whmmb3vnMZ7FyCkhrCzg10ZvY1UpAdI\nAGrlVIKuBnROTk5ubq6enp6dnZ2mu9kRQggvdCzaYmNjx4wZ4+DgYGFh4ezs7OjoKJFInJ2d\nR44cGc715ySEkGpBl1rQM2bM2Lx5M8Mw7ID91tbWADIyMpKTk0NCQkJCQiZOnLh9+3a1b5c9\n9GxYjXrmE0JKEOYZJp0J6C1btmzatKlnz57ff/99q1atSsy9d+/e8uXLd+zY0bRp0zlz5qh3\n023btr1z507FJxIB+Pn5TZs2zcvLS71bV11qaur8+fM3bNhQu3Ztvmq4du3avn372Lsr8OXX\nX39NSkqaP38+jzWsXr26Xr16Q4cO5bGGadOmjR492sfHh68CMjMzZ86cuXr1auV71GnZnTt3\nNm/efOXKlYoXE4vFLVu21E5JlcPfUNSVw+OA/SoyMTEJ5fWeQg8fPgSQkpLCYw0HDx60s7Pj\nsQCGYb766qvAwEB+awgMDPzqq6/4rcHOzu7gwYM8FpCSkgLg4cOHPNYQGhpqYmLCYwFVpDPH\noGnAfkJITaMzAc0N2F/BMtV8wH5CSA2jMwFdcwfsJ4TUVDpzknDq1KkxMTHBwcFhYWEVDNg/\nb948vislhBD10JmABrB169bPPvuMHbCfOy3LDtg/YsQIzQ3YTwghvNClgAbg5eV14MABaHfA\nfkII4YWOBTRH+AP2E0JIFVHbkxBCBIoCmhBCBIoCWm0kEgm/l/NLJBKRSMR7DbyPaUA1CKQG\n+kBWXfUZsJ93T58+rVu3Lr9nLB8/ftygQQMeCyguLk5JSalXrx6PNbx9+/bdu3e2trY81vDq\n1StjY2N13Qb+wyQlJTk5OVVw8a0W8P6BlMvlz549c3V15bGGqqCAJoQQgaJDHIQQIlAU0IQQ\nIlAU0IQQIlAU0IQQIlAU0IQQIlAU0IQQIlAU0IQQIlAU0IQQIlAU0IQQIlAU0IQQIlAU0IQQ\nIlAU0IQQIlAU0IQQIlAU0IQQIlAU0ERTEhMTN23axHcV/KjJ+y5Ab9++3bNnT3JyMt+FVBoF\ntDo9efJk5MiRbm5uJiYmnp6eX375ZXZ2tjYLKCws/M9//tO5c2cLC4uGDRuOHDny0aNH2ixA\n2caNGxctWqTljW7dutXPz8/S0tLPz2/r1q1a3jqHl31nCeEzwPsXoYQZM2aMHTs2Ojqaxxo+\nEEPUJCEhwcTERCwWf/TRR1OmTPH29gbQvHnz/Px87RSQlZXVqVMnAM2aNZs4cWKPHj1EIlGt\nWrWioqK0U4Cys2fPGhoaWlpaanOjU6ZMAeDu7v7pp582btwYwPTp07VZAIuXfWcJ4TPA+xeh\nhEOHDrFZFxoayksBVUEBrTaDBg0SiUQnTpzgpnzxxRcANm7cqJ0CFixYAGDatGnclJMnT+rp\n6bVs2VI7BbBGjRrl7u7OfiW0GVJRUVEAAgMDpVIpwzBSqZSNp5iYGK3VwNe+c4TwGeD9i6As\nOTnZysqKvfcYBXSNZmdn16ZNG+Upd+/eBTBu3DjtFNCkSRMzM7OCggLlid26dQOQlpamnRoY\nhhk4cGCfPn369OljZmamzZAaMWIEgOjoaG7KrVu3AHz66adaq4GvfecI4TPA+xeBI5fLP/ro\no/r16y9cuFBHA5rPG0pWJ3K5fNGiRSVulpqWlgagUaNG2qlBT0+vS5cuhoaGyhPZWxpnZmZq\n7SaqR44cYR94enpq87TMH3/84ezs3KJFC25K69atHRwczp49q7Ua+Np3Du+fASF8EThr1669\nePHiX3/9FR4eruVNqw3fvxDV0Lt371JSUk6dOuXm5mZnZxcfH89XJa9evTIyMrKzs2P/6tcy\nDw8PrbUiMzMzAXTs2LHEdPYAaE5OjnbK4Ghz3yvG42eA3y9CVFSURCJZsGABwzArV64EtaAJ\na86cOcHBwQBMTEwuXbrk5ubGSxnx8fG9e/cuKCjYunWrWFzN3+jc3FwA1tbWJaazU3JycszM\nzHgoi2/8fgZ4/CLk5+ePGjWqWbNmS5cu1dpGNaGaf2814d27d9u3b+f+2ahRo969eysvMGXK\nlICAgMTExG3btvn6+v7yyy/9+/fXZgF5eXmrVq1avXo1wzCbNm0aO3asGreuYg1aZmBgAEAk\nEpU5V0+vxnUn1cJn4L00/UWowPz58x8/fnzz5k328I4O47sJr3tSU1OVX8DBgweXt2RKSoqZ\nmZmTk5M2Czh16lTdunUB9OnTJy4uTr2bVrEGljb/zJfJZPr6+p07dy4xZ4cDrgAABPxJREFU\n3cfHR19fXyaTaacMDr+HOLTzGVCdhr4I5fnzzz8B/PDDD9wU3T3EQQGtHomJicHBwaV7dAUE\nBADIyMjQThmLFy8G0Lx587/++ks7W6yAlkPKwcGhQYMGJSa6uLhoLReU8RjQ/H4GhPBFWLNm\nTQVN0h07dmihBnWhQxzqkZaWNmXKlJkzZ65fv155+uvXr01NTS0sLLRQw549e7755pvhw4fv\n2bNH5/+yqzx/f/+QkJD4+Hj2EhUA9+7de/78Odv9robg/TMghC9Cy5Yt2UuWOFFRUZGRkb16\n9apXr16TJk20UIPa8P0LUU0UFRXZ2tpaWFg8evSIm3jw4EEA/fv310IBcrnc3d3dycmJr+u1\nStNyK/LixYsAPvnkE/afcrl82LBhAC5fvqy1Gji8tKCF8Bng/YtQJt09xEEtaPUwMDDYuHHj\n8OHDPT09g4KCbG1tHzx4cOHCBTs7u82bN2uhgKSkpIcPH9apU2fgwIGl5+7bt8/GxkYLZfCo\nS5cuY8eO3b1794sXL3x8fK5cuXLp0qUJEyb4+fnxXZqWCOEzwPsXobrh+xeiWjl//nxgYKC1\ntbWxsXHLli3nzJmjtaPP586dq+BdTk5O1k4ZyrTfipTL5f/97399fX3Nzc19fX3ZPgy84KUF\nLZzPAI9fhDLpbgtaxDCMmiOfEEKIOtS4/qGEEKIrKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSg\nKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSg\nKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSg\nKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSg\nKKAJIUSgKKAJIUSgKKAJIUSgKKAJIUSgKKAJAYB79+4ZGhoGBARwU6RSqaenp7W1dWpqKo+F\nkZqMApoQAGjevPnChQsvXry4a9cudsrq1atjY2M3bNhgb2/Pb22kxhIxDMN3DYQIQlFRUZs2\nbV68eBEXF5edne3p6dm9e/cTJ07wXRepuSigCflHZGSkr6/v8OHDU1NTo6Ki7t275+DgwHdR\npOYS810AIQLi7e09a9asH374AcDevXspnQm/qAVNyL8kJia6ubmZmJi8ePHC3Nyc73JIjUYn\nCQn5l7lz50okkry8vAULFvBdC6npKKAJ+cf+/ftPnDixcuXKwYMHb9269erVq3xXRGo0OsRB\niEJaWlrz5s1dXV0jIyPT0tKaNm3q7OwcFRUlkUj4Lo3UUNSCJkRh6tSpWVlZ//vf//T19R0d\nHVesWHH//v2VK1fyXRepuagFTQgA/PLLL8OHD587d+6aNWvYKXK5vEOHDtHR0VFRUU2bNuW3\nPFIzUUATQohA0SEOQggRKApoQggRKApoQggRKApoQggRKApoQggRKApoQggRKApoQggRKApo\nQggRKApoQggRKApoQggRKApoQggRKApoQggRKApoQggRKApoQggRKApoQggRKApoQggRKApo\nQggRKApoQggRKApoQggRKApoQggRKApoQggRKApoQggRKApoQggRKApoQggRKApoQggRKApo\nQggRKApoQggRKApoQggRKApoQggRKApoQggRqP8HM9zuoArcQAAAAAAASUVORK5CYII=",
      "text/plain": [
       "Plot with title “Normal: Red, Mixture: Blue”"
      ]
     },
     "metadata": {
      "image/png": {
       "height": 450,
       "width": 600
      }
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "w = 0.2\n",
    "mu1 = -1\n",
    "mu2 = 1\n",
    "sigma1 = 0.8\n",
    "sigma2 = 0.5\n",
    "\n",
    "xgrid<-seq(-3, 4, 0.01)\n",
    "nm <- dnorm(xgrid)\n",
    "mix <-w*dnorm(xgrid, mu1, sigma1) + (1-w)*dnorm(xgrid, mu2, sigma2)\n",
    "plot(xgrid, nm, \"l\", lwd=2, col='red',main='Normal: Red, Mixture: Blue',\n",
    "     xlab = 'x', ylab = 'y', ylim=c(0, max(nm,mix)))\n",
    "lines(xgrid, mix, lwd=2,col='blue')"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "6e581b11",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "The idea\n",
    "\n",
    "-   Let $f_y(x)$ be the **target distribution** and $f_v(v)$ be the\n",
    "    **proposal distribution**\n",
    "\n",
    "-   Simulate an $x$-coordinate from the proposal $f_v(x)$\n",
    "\n",
    "-   Simulate a y-coordinate from $U(0, M*f_v(x))$\n",
    "\n",
    "-   Reject any points that are not ‘inside’ $f_y(x)$"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 9,
   "id": "f2d44d6e",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeAAAAFoCAMAAAC46dgSAAADAFBMVEUAAAABAQECAgIDAwME\nBAQFBQUGBgYHBwcICAgJCQkKCgoLCwsMDAwNDQ0ODg4PDw8QEBARERESEhITExMUFBQVFRUW\nFhYXFxcYGBgZGRkaGhobGxscHBwdHR0eHh4fHx8gICAhISEiIiIjIyMkJCQlJSUmJiYnJyco\nKCgpKSkqKiorKyssLCwtLS0uLi4vLy8wMDAxMTEyMjIzMzM0NDQ1NTU2NjY3Nzc4ODg5OTk6\nOjo7Ozs8PDw9PT0+Pj4/Pz9AQEBBQUFCQkJDQ0NERERFRUVGRkZHR0dISEhJSUlKSkpLS0tM\nTExNTU1OTk5PT09QUFBRUVFSUlJTU1NUVFRVVVVWVlZXV1dYWFhZWVlaWlpbW1tcXFxdXV1e\nXl5fX19gYGBhYWFiYmJjY2NkZGRlZWVmZmZnZ2doaGhpaWlqampra2tsbGxtbW1ubm5vb29w\ncHBxcXFycnJzc3N0dHR1dXV2dnZ3d3d4eHh5eXl6enp7e3t8fHx9fX1+fn5/f3+AgICBgYGC\ngoKDg4OEhISFhYWGhoaHh4eIiIiJiYmKioqLi4uMjIyNjY2Ojo6Pj4+QkJCRkZGSkpKTk5OU\nlJSVlZWWlpaXl5eYmJiZmZmampqbm5ucnJydnZ2enp6fn5+goKChoaGioqKjo6OkpKSlpaWm\npqanp6eoqKipqamqqqqrq6usrKytra2urq6vr6+wsLCxsbGysrKzs7O0tLS1tbW2tra3t7e4\nuLi5ubm6urq7u7u8vLy9vb2+vr6/v7/AwMDBwcHCwsLDw8PExMTFxcXGxsbHx8fIyMjJycnK\nysrLy8vMzMzNzc3Ozs7Pz8/Q0NDR0dHS0tLT09PU1NTV1dXW1tbX19fY2NjZ2dna2trb29vc\n3Nzd3d3e3t7f39/g4ODh4eHi4uLj4+Pk5OTl5eXm5ubn5+fo6Ojp6enq6urr6+vs7Ozt7e3u\n7u7v7+/w8PDx8fHy8vLz8/P09PT19fX29vb39/f4+Pj5+fn6+vr7+/v8/Pz9/f3+/v7////i\nsF19AAAACXBIWXMAABJ0AAASdAHeZh94AAATy0lEQVR4nO2deXwUVbaAb6eBhKyExZCQsIRV\nBAXjsAUUkGGQhyzCjAQYBZ9oGBBkURQFcRgQBUEBGYnLMDrvyfJwHHFhgEGQicNjDRAYISiI\nJICiAVkkhHRNVSfpdCfd1aeqbt3OPZzvj06RPnVyqO/X1bXde5hCoIaFugDCXkgwckgwckgw\nckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgw\nckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgw\nckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgw\nckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgw\nckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgwckgw\ncqwJvnCqoIRTIYQ9WBB88IGGjDFno4x/8iuH4I15wRMcLLFz//5dkhl7WDcwZzfBiRzjmkwL\nfo39am/pUu797GWdwF2M4MYuw55MC+7Wurh80dUjXScwmxWZ/RuEL0Us2/A6pgXHPlixPCNO\nJ5AEc0Oo4G5trnuWe9EnWAhCBb/G7jlQunRkBHtJJxCP4OIfQ1yAUMFKJmMp3QcOurMZY6Nd\nOnFYBH/YJ5zFDNsRyhLEClb2ZdRXj+uciRlbdcNwCC4cVOvhT3avHRw26VroihAsWKXw5Omg\nV7JQCD59yy257oVNN93zc8iqEC8YAgbB59t3PV+2+FWTgdd1Y22EBNtEyX/dXHF89WXd6aGq\nI1SCCzt0qPSbE4nxHqLZFQ5/I6S8FHvU61+fOjeEqI5QCT7HKme5/sEaD2PZRQ5/I5Tkhr/j\n8+8pjQpDU0ioBF/bvFnn3ddlF+xKH+D7iystM0NTSfX8DpZe8Mqobyr9ZqNzb0gqCY3gH4Oc\nKMku+HLS76v8bnCvEBQiWvDPS8fMPar8NYlFD8rXi5Nd8Nyky1V+d6TGpyGoRKzgwraMsYQ9\n4bG92rEEvYu0kgsujF/u57cP36F3ddYuhAqexqYc2NQiqrH66X2PTdUJlFzw75v4O40/Uesj\n4ZUIFty2i/ryMZunLfesfB7sjdyCL9bz9wFWP8LdBBeiIVRwbe1U4RRboy2Pi9QJlFvwoob+\nLz0fCdsuuBJFsODUu9WXK5nux8CG1tcJlFpwceN5Ad4ZMlhoIW6ECr6/5ofli8dq99cJlFrw\n6qhAx4/bw44JrURDqOCvIh1p67WFgxPjHJ/pBEotOH1cwLdunyKwjlLEngfn3ZewTPv5OktY\noxcns+C9jkMB3/tTnUsCK3Ej/EqW+xrWsWz9ZxxkFjxW54rVlbpviiukFLoWzZnzUat13p3c\nSVghZZBgzixP0Ns5HWYmRpJYggRz5vYndd/u/pigOsohwXzZ5zii+/7bda8KqqQMEsyXx7rr\nv38xWvf0gT/VR3DJZ5s8TJJVcFG9t4JEPKh3gccGqo/grxtUPHQXyX6y5W/YzrrIC0EiPqtx\nWkgl5VQfwd5Iu4sePDJYREmTRSIK8UCCeXKuVvCnY5++XUAhFZBgnryWGHwEQy77t4BKPJBg\nnqRPBgTdNtP2OrwgwRz52gGZD+PFFrYX4gUJ5si8VpCobxw77S7ECxLMkfbPgcLSRd4VJsH8\nOMS+BMUtTRY41R8J5sfMjrC4AqfAh+9IMD9avggM7CnwlhIJ5sZux9fAyOWJ4vbRJJgbT3aG\nRp5xbrOzEB9IMC9czfRm3/Sll7h9NAnmxU5H5SHBgVmeJGwfTYJ58URXeOxpp7D5skkwJ1zN\njNwGvGuSbYVUggRzYqfjpIHopcmixgqTYE480cVIdH7Yv+wqpBIkmA9GjqE10qfZVEhlqo/g\n70f+2kOadIJ3GTiG1liUalMhlak+gs9PfMRDD+kETze0h1aUEw5BsypVH8HeyLeLbr7Q4Ap3\nPGNLHVUgwVzY4zhucI0XbrajjqqQYC48ZXjU4FF22I5CqmBdsB2t6qQTDL5TWEH7qpPh2YFF\nwTa1qpNNcA77yvA6s2+zoZCqWBMMblVnENkEP5NmfJ2DLI9/IVWxJBjcqs6XkqOHivUjZBPc\n6gUTK7U2vls3gSXB4FZ1ZTyrDb0rfjGasfBHzusFSiY4h5mZHulpIdM5WBIMblVXvmJP9eUx\nFj/s0S6srd5AaMkEP2NquNFuQ7cnzGLtEwxtVVe+oio419HpnLr4FpulEyiZYFN7aMXVdDHv\nQvxg8TsY2KqufEVVcBb7wr2c/gudQLkEm9tDK8qUILMBcMHaUTS0VV35iqrgWWXuMmN0AuUS\nbOYYWuOLsAK+hfjD4nkwsFVd+Yqq4HdZaTuwwe11AuUS3HK+ufVcycv4FuIP61eyIK3qyldM\nmrN2Z4Ph2uLOmg/pBEoleC/4eejKTOrJtRC/CL0WneJw9xzfoihP1a6ndwgpleDp4OehK7Pd\neYZnIX6xIniHL4A1rxz4vxce6v65orRJ0d2nyyTY2NN2PpQk+Z8anidWBDNfjKQ4pL9Xl0nw\njrBvTa87oTfHQvxjTXDs8GkVcKxKJsGP9zC/7jb799FWBM9oxRxdXz7Oq5RLP3pYJI9gS7tZ\nAftoawdZB2e3ZyzthaM6wQGo2n30WJj3/l6aidC21PjOwtqP2X4cbfko+si8NMbaP59rMEfV\n7qPKgd0eZsjzCR7bz8ra222/1sHjNOnEy90crLWxh8iwdB+9Gv9nK6u7UpbwqiQAnM6DT40x\ndhQdBHkEvx9p7ctkqt3NsrgI3vlkM/Vwi0s9pcgjeOhwa+vvcpzgU0ggLAt27ZjahIV1f9X8\nyaAfpBFcGPGxxQwtbH6uw5pgV/bjySys5zLeRwrSCF5xU5CHj4IyU6+HIwesCP58YhJz3v1H\nG87VpRHc3fI438MscJslHli7khUzYu1WD0HXW1rHB51IWQTnOfZYztHR3jEsIq9F500MZzHt\nPOhEyiJ4pt5NbSALm9k6FtyK4Nm+ANbcwAaA/oIkgkuaGBsU7JcC5+fWkwRG8NikVqgEb6x5\nlkOWvmM5JAmIYMEjh4DCJBE8/D4eWd6t47+fNB9odKF5zoV/xCPNpRi9bodWIcHmWZQcvEMD\nhNH3cEnjHxJsGtfNz/FJtNV5ik8if5Bg03zm5DT0xNXc1MgIGCTYNPcP4pVpbkv7ToVJsFkK\nAE2wgOTX2MIrVRVIsFmea8XvYzcwg1uqylQfwVffWuFhpI/gn/69bd2bi+c/M3369Jnzl6z8\nW/axK7ZUYIirDV/ll2x9+Pf8kvlSfQR/2ynNQ2Pvh+5uZYzFp3bs2kejU/smMeq/G9wx/Nn3\n9us1U7ebP8cG6zNqgOtNAGMzzVF9BHvjs4vO2VXge7559WT2qvlj76rPanUc+2auwBY13nSA\ndLEDM6e5Xf8NCQQH5OzG+UOTWd2Bi/eLmpu3go01jvNMd7qW1SdDAiGzYDff/s+jrVjD0at1\n5/zgzy85HxaNsOtqlvSCNb55Y2hszT7L8u0qpyq7HDl8E+5wwLqmGQaFYJVrmyakhKW/KmDI\nvJsh/Xln7DKed8ZSsAhWtOc7p6Q4e7/N8eA2IAfCvuCdcnXUD7xTukEkWMW1fVy92iP+bvuB\n9bC+3FMWN53DPacGLsEqRX8dVDNl1nF+tfhhrx0dF15NsOXyDTrBKt8tahvWd52NV0H63WtD\n0kv1bZmSBaNglewxkYnPGuuiAOcfzgN2pJ3TuMiGrEgFK0rhkrbOQRvsuAJS0kFvgiDznK+T\nZUNWtIJVtv6mZqvF/C+AZEXbdMI9q6kNH2HMghUlf3Zi9DijY9OD8EMDk/OeBaUw3oYJHXAL\nVpRr76U77v6A53nT2DZ2fFW6mZd0mXtO7IJV9oyOaLawkFe2rWGgWRtNcSnxD9xz3gCC1fOm\nuY2iMvkM4rvU4lEuefzzRgz3oZo3hGB1T71a21NzeIz50aZ2zv9z/VbuB+g3iGCVPWMimr5k\n9Xrv+85tXIoJxJaw/+ec8cYRrO6p56XUfsjSgN68Os/zKiYAw9P4jJbwUH0E53cN8EwWR4rX\n9XZ0ecf0WK+f2vWz+z5GQZzpqU39U30E//zKfA9D7Hts9vCEuHrTTEzNp1Lcv9WPnKupSlaU\nuf4Agag+gr2x9bnoS1lpjt6r9Jq++Mf1YAMBraxcfbpz3UnfgIJVdo6Nrvf4QWPrlDwSt9ue\nanw5WYfryfCNKVj9On2jK0tbeg6+QtHIOpApzzmwqsZ2jtluVMEqh59IqjVoDfCI6/u7EvfZ\nW04FmUmn+SW7gQUryvUNo6Jjf7secG3585SOdt1drsrVzl2NHyEEQrxgSL9hcYPPLr03OCJu\n1Fr9P3dhojNT5HCo/OQMbqdjggUD+w0LHV144X+HRYf3fSVgQ+7Lr9yUym2kKIz9cRN5pRIr\nGNpvWPTw0aufTmjOGo3K8jPQaf+0+g0W2DkNjl+21X6SUyahgsH9hkMxPvhY1ogUFnvn+D9u\nzCvbHf+w662xqewXK/jfpA3OpshJfPbSQgWD+w2HagD4qXXPDmpZk7GohqmpDSMYSx68hO91\nJThb437D5WtfqGBwv+GQjvAvPvmv9WtWrFjzSY7gAW2+HGicxmOucLGfYGi/YRmmcLCds73i\nV1nPIvg7GNhvmARrXP9DzfssT6Qv9iga2m+YBJeS0ylqpsXvCcHnwcB+wyS4jJKVjeNnWHoM\nW/yVLEi/YRLsoSirTY2Ba8yfqd3Q16LlwLV5VHTt/ov3mGv/QYJl4MqH41qzyC6PLP7okNEN\nEyrBVZtTKrlS9i4Uxpn1z/+6fQRjMa3TB/x2/PR5C1dkrVmzbpPK5t2V8ZolNVSCqzanPObw\n7vARisuDMlCw829ZcyY/NKxPt7SWqUnx8XWYP5pXrBAqwX6aU/5U0T94A7Nt/A9OvLadhtfN\nker5HZxNgnlRPW/4k2BuVM8b/iSYG9Xzhv8uv4cOhCl2iRMMvuGv5Hgd80dMfRfKArYEHDs+\nFhz67r23wmNvvRceGzseHLqELQDHTo3w2nwm5ly0/4a/D1Hw7kRHGPy67aoEcKjyVD94bL+n\n4LEJ8PuB+ewIOPajKHgJ/rD/hr8PJFhDCsHgG/4+kGANKQSDb/j7QII1pBAMvuHvAwnWkEMw\n9Ia/DyRYQxLBCuyGvw8kWEMewYYhwRokWIMEuyHBGiQ4IIIFx28Ehx53wFvEvZ8CL2HWQHjs\nwFnw2JT3waHfO46DYzfGw0vwh2DBxw0ck30FDy02MDDk4ll47FkDTxudMPAgnYH/WslxeKw/\nBAsmREOCkUOCkUOCkUOCkUOCkUOCkUOCkUOCkUOCkUOCkUOCkUOCkUOCkUOCkYNHcN5SOXIa\n5uJKKzOoiRb8dUaLyHZPgCYEuzqjR2xqBngC0Yl1QGHL0+PSwZ1fgTmN1WpgE7gZzeDPOVVF\nsOC8qBq9MzuzWwCTNp/vwdo+3NdRG9heYWM4SEYma/1AKzaBa05jtRrYBG7WMpkED3V8qL5O\nZoBd39NsvPr6cdhtkLwjWzMGkbGP9StWivs6IG14oDkVY7Ua2AQap+pGyyQ4IU17PcDGBA9t\nE+PuZtGHQZ6hGjJgQAxERgbbr77uYQ9wzKkYq9XAJlBx9W42QyLBJcvWaz82sbnBY9sOcP/o\nz76E5W4HkVE/2f0jsSHHnIqhWo1sApUFYdvnSyRY40r+Jy0TwA0Hv4tIAD6tCJFRyEoHunYG\nNsyECi4FXCt8E+yr9bQim+BMxqLAfWGPtGB/AoZCZJxkpQ9F92enuOX0AK8VvAmutO1QJIfg\ny6+olNaZs3pu4/APQKGXZtWOWAZMC5Jxmg1y/+zPCgBFGxIctFYvgm0CD+MjchU5BJ/RpogZ\nVv6v/JhGkNBPGrMB+l9q3mkhMkqcd7p/dnHCHsCHCw5eqy+6m6CczWyxIongMo69Xnp+0osB\nmvfOYrcY6cEOkpGY6v6RAti64Jwa8FqNbIKFnumT3gTWURWxgrNZaRewdtHBP0Er2XBDM6iB\nZGS4h33lsgyOORVDtRrZBJsyNTqzezL155rTQ6zgazfFacNyVpV9Ferhat3IWI8ykIytbJSa\n+n4GbPoKFGykVgOboAyZdtHKakfksN/1YgnBD2KPswb9SgEOMoTJGM16z7iT/TcsJVSwoVrh\nm6AMqQQrW/rVi7xtCuAb+B+e7x/gloDJcL3YLbbbAlhGsGBjtYI3QRlyCSYEQ4KRQ4KRQ4KR\nQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KR\nQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4KRQ4IVJbdWT/X1\nWru6p0NdiQ2QYJXZ7G1Fmcv+Euo67IAEqxS1q/tdXsS9oS7DFkiwxo6wEb3jYTMMywYJdjOZ\nsXdCXYM9kGA3eSzqQqhrsAcS7GZgLfa7UNdgDyRY4y9s0TBHdqirsAUSrHKmXtr1/Ni2huYf\nlwUSrHKfc4+iLGPPh7oOOyDB2uzrU9XXkk7hh0NdiQ2QYOSQYOSQYOSQYOSQYOSQYOSQYOSQ\nYOSQYOSQYOSQYOSQYOSQYOSQYOSQYOSQYOSQYOSQYOSQYOSQYOSQYOSQYOSQYOSQYOSQYOSQ\nYOSQYOSQYOSQYOSQYOSQYOT8Bz0IJjcz0qwjAAAAAElFTkSuQmCC",
      "text/plain": [
       "plot without title"
      ]
     },
     "metadata": {
      "image/png": {
       "height": 450,
       "width": 600
      }
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "M0 = (w*dnorm(xgrid, mu1, sigma1) + (1-w)*dnorm(xgrid, mu2, sigma2))/dnorm(xgrid) \n",
    "plot(xgrid, M0, type=\"l\", xlab=\"x\")"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 10,
   "id": "4334f112",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeAAAAFoCAIAAAAAVb93AAAACXBIWXMAABJ0AAASdAHeZh94\nAAAgAElEQVR4nO3deXgM9x8H8Pfmvg+55JJIQhAR9xGCVN1VtwRFtLTum6Ko0rqPuuq+qoTy\nawnaat0EcUVIlCCEJBK573vn98dsx8p97O7M7n5ej8eTzMzOfGZ29p3Zme98R8QwDAghhAiP\nBt8FEEIIKRsFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGE\nCBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGE\nCBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGE\nCBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGECBQFNCGE\nCBQFNCGECBQFNCGECBQFNCGECJTKBnRubu6mTZv69OnTuHFjAwMDe3v7Tp06ff7556GhoXJd\n7s6dO0UikUgkMjY2ltU8z507J/pPcnKyrGarXGq/YRMSEkTlMzAwaN68+YIFC3JycmRVcy3f\nuG3btklXqKGhkZqaWmIaKysr6WnGjh3LDpfHfihw2dnZ5b25tra2HTt2XL58eYk3V/hbSYvv\nAuTi4sWLI0eOjI+P54bk5ubGxcUFBwfv379/yJAhhw8f1tHR4bFCIjS5ublhYWFhYWFnz569\nd++etrY23xWVxDBMSEhIr169uCFRUVFJSUkyX5BYLO7fvz/787x583x8fGS+CAWLj4+Pj4+/\ncePGrl27rl+/7uTkxHdFVaWCR9Bv3rzx8/Pj0llDQ8PS0lJTU5Ob4MSJE3PnzuWpOiJ0jx49\n+vHHH/muomy3bt2S/vX27dvyWArDMGf+ExcXJ49F8CUmJsbPz6+4uJjvQqpKBQN6/fr17GGF\nlpbW9u3bs7OzExMT8/Ly/v7770aNGrHTbN68+dmzZ7yWSfi0cOHCov8UFhYmJyf/9NNP3Nig\noCAea6vAzZs3pX8NCQkpb8ovv/ySXbu0tDT51yU406ZN497f3NzciIiIfv36saNCQkLkfZ5T\nhlQwoO/du8f+MGrUqAkTJujp6QHQ0tLq3r37mTNnRCIRO/bOnTu8lajqxGIx3yVUQkNDQ/M/\nWlpaderUmThxYpcuXdixERER/JZXWr169QCEhIQwDMMNZAPazs5O+gsiSyQScStYrQU9e/ZM\n+jj92bNnISEhWVlZNS+dD9Lvr56eXpMmTfbu3cuNVaLPvgoG9Js3b9gfuCzmuLq6fv/993Pm\nzJkzZ46FhYX0qNTU1K+//rpbt26Wlpa2tra+vr4bN24sLCyUnqawsHD//v2+vr7Ozs56enr1\n6tXr2LHj5s2bq7j7hoWFjRs3rlWrVkZGRm5ubn5+fjdu3Cg92fPnz4cNG2ZlZWVtbT1gwICT\nJ09Wfd2/++479qJHgwYNxGLx+vXrPTw89PX1nZ2dBw0a9OTJk9IvKSws3LBhQ//+/V1cXExN\nTb29vb/88stHjx5VMGcAv//+e4sWLdzd3QHMnDmTHeXj4/Pw4cOOHTtqaWnp6up6enru378f\nQH5+/g8//NC1a1dTU1M3N7fPP//87du3JWqo8YZ99uzZd/95+vRp1bdVadypyRJ7jgLeuEp1\n6NABQHp6+r///ssOKSwsZI8EO3ToUHpXL335KyQkRFNTk3unuClnzJjBXUzbuXPnwoULO3Xq\nxI1dvHhx+/bt2b9Y48ePZyfz9fWVXtbevXvZ4dIn7ivYYVhV3KoyfH85derUqWBstVaTVcV1\nqQlG5Xz00Ufsqmlqan733XcxMTGVvuTChQt2dnalN467u3tCQgI7TV5eXvv27cvchp6enpmZ\nmexkO3bsYAcaGRlJL2LDhg1lXpacN2+eWCzmJrt06VLpvWfo0KHcz0lJSRWsyNKlS9nJXF1d\nhw8fXmI+urq6YWFh0tM/fPiwWbNmpavS1tb+9ttvpQvj5uzm5vbLL7+wieDs7MwwzIwZM9hR\njo6OZmZmJWa1bt26Ejs6AHt7+7S0NJls2DNnznDTnzx5soKNI33ReNGiRaUn4GKrQ4cOCn7j\nyrR161bu5Zs2bWJ/2LNnDzv27t277JC1a9dqaUmu9gcEBFSwuWbPns3NMCgoiGGYV69ecWvX\ntWtXsVg8ZMiQ0it769YthmHGjRvHTSld5549e9jhWlpa3MAKdpiqb1WmOu+v9J/zGTNmcMOL\niooiIyMHDBjAjnJwcMjOzq5gK1VrNau1LjWgggH9yy+/lNhS9evXHzZs2IoVK/7666+cnJwS\n0ycnJ3MfLW1t7ZYtW7Zo0YJ7bY8ePdjJ5s+fzw1s1KhRly5dbGxsuCFLlixhJyvzLT937hw3\npbe399ixY9u0acMNWbduHTtZYmKidHOfunXrGhkZlViXKgY0i21gxH16AfTs2ZObOCcnx8XF\nhRtVr169Nm3a6OrqckP27dtXes42Njbcl48SAc0yNDQ0MDBAKZaWltK/Llu2rPYblpFRQKen\np+/atYsbu3//fgW/cWWSDuibN2+yJyvGjRvHjt22bRs76vr161UM6JycHDc3N3Z406ZNi4uL\nx4wZw/5qYGDw/PlzdrKioiJuuUePHuVeXrOALr3DVHGrsmoW0OVxdnZ+9OgR95LaB3S11qUG\nVDCgGYZZvHhxec2k9PX1Bw4c+OLFC27iqVOnsqMsLS25N+/o0aPcSx4/fswwTOPGjdlfFy9e\nzL22d+/e7MBevXqxQ0q/5UVFRU2aNGEHSufCokWLuCmTk5MZhpk5cyY7xNDQkD3AKSws/Prr\nr6Xrr3pADxw4MDExkWGYpKQkbqcxMTEpXYCGhsbevXvZgXFxca1bt+Y2SEpKSuk56+joTJw4\ncffu3UeOHGE+DOjFixcXFxdnZ2dPmTKFG1ivXr0nT54wDPPw4UMuuQYOHMjOucYbllWzgK7A\npEmTFP/GlUk6oMPDw5s3bw7Aw8ODHctmq7a2dk5OThUDmmGYK1eucOdD5s6dq6EhOcm5YcMG\nbhrZBjQ+3GGqvlVZsg3oJUuWSB/V1jKgq7suNaCaAc0wTGRk5PLlyzt37ix9SMgxMDBgv7Ux\nDMOdeVywYIH0HHr06OHm5ubm5hYYGCgWi4/+h009hmEyMjI6d+7MvrZ169bswNJveXh4ODuE\nvdGAm39GRgb3uQoMDGQYhjsK4w4bWdJH9FUMaB0dHe7kAMMwhw4dKj0Hrk3LiBEjpGfy6NEj\n7jP822+/lZiz9EAWF9BWVlbFxcXswKioKG76TZs2cROPGDGCHdipUyeGYWqzYaurKgEt/TFT\n5BtXphIBPWnSJAAikYg9O8S+fez2qXpAMwwzefLkEmvdrl077o1j5BDQ0jtM1bdqdVXxUtCo\nUaO4l9QyoOW3LhwVvEjIatCgwaJFi65cuZKVlRUWFrZv377Ro0ebmJiwY3NyctjdNC8v7/Xr\n1+xALhRY586de/bs2bNnz/z9/UUikZ+f3+DBgx0cHLZv3z5s2LDmzZtbWVldvXq10kq4S3Ni\nsdjc3Jy7IGNiYsJ9Ep48eRIbG5uZmcn+OmjQIOk5lD6bXCkHBwfpb9l169blfmYXWlBQ8Pz5\n8zIX17RpU/bCDgDukhTH2Nh44MCBZS60Xr163BEZt6kBcF+rSwwHUJsNKw/ff/89d+zPyxtX\nAfY6IcMwt2/fTk9PZ6+YsQOrZdWqVdJ3aujo6Ozbt49742SuxA5Txa1ay4VKN7MrLCyMiYlZ\nvXo1O+rQoUP79u2r5fxZClgXlQ1ojpaWVrNmzcaOHXvw4MFXr15x16Pu3buXlZX1+vVr5r92\nS9bW1hXM58GDB15eXp06dVqyZMmJEyeys7MHDBjAfROvQHR0dKXTpKSkSF+htre3lx5bv379\nSudQQonPW+mr/LGxsdw+VGJxABwcHNgfpA+EWRVspdJLYVXc0qvGG7Y2pI+Ui4uLX7x40aNH\nD3bUtm3b2PeClzeuAt7e3uwPN2/evHPnDrvflnd9tQJGRkbswTirb9++3Pd0eSixw1Rxq9Zy\noSWaUdrb28+bN4+7PZI7cK4lBayLqt3qHRsbO2HCBPbn2bNnd+3aVXqsubn5zJkz/fz82F8T\nEhJsbW25sRX0lpCfnz948GA2rfz9/X/88Uf2QtbChQv//PPPiktydHRkfzAzM5M+oSbN1tZW\n+p7dt2/fSl9S4w7QZMje3l5LS4vN6NJ3i8XGxrI/cMVzykvhmqnNhpUVDQ0NFxeXZcuW/f33\n3+yQiIgId3d3ob1xLi4uNjY2CQkJt27d4v7m1eAIOjk5ef369dyvQUFBt2/fbtu2bdXnwEi1\nxa5UiR2milu16vOvuiZNmpw6dQpAZGRkVaavdDUVsC6qFtC2trbXr19n754yMjIqEdCQaiVt\nZGRUv359DQ0NOzs7NqGuXbvWvXt3bspPP/305cuXAJYuXero6MgdSy5btoxrZlC6vXBpXNvP\njIyM5s2bGxoacqMSExPZezqMjY3Nzc254b///runpyf369mzZ6u08tWho6Pj6urKHv39/vvv\n0t/NHz9+zN1m6eHhIfNFSwsLC6vxhpUt6aYjbJ9EAnzjOnTocPLkSS6gra2ta3CQPnXq1Hfv\n3nG/FhcXjx079v79+2VerZHG/VUocShTolV7xaq4Vas+w6rjzjaUPuyQVvXVVMC6qNopDg0N\nDS6Ujx49OnnyZO4Uc25u7oEDB7799lv217Zt27LnAbjvtlu3buXuAQ0MDDx9+nR4eHh4eHjL\nli0zMjK4RXBN0M+cOVOVT2Djxo3ZT5FYLF6yZAk3/MCBA9bW1nXr1rWzs4uOjjY3N+fO/K5d\nu5ZtvsMwzObNm//3v//VaGNUggvlI0eO/Pzzz+zP8fHxAQEB7L5lZmbG3VwnJ7XZsCxZ3cgg\nfVNSdnY25PbGBQcHcwWnp6dXq0j2LEdqaip7sF+Dw+dTp04FBgayP69fv55twPv48eNly5aV\nOT27KVjcmeuIiAj2UBTAhQsXpI/HK1XFrcoNl8n7m5iYuHHjRu7WIemWcKVVfTWruy41UZsr\njMIUHR1tZWUlvY5GRkY2NjbSp2WNjY0jIiLY6ePi4ri/ctra2m3btuXamQEYOnQowzDx8fHS\nL/fy8vL09JT+7ta0aVN2bmVeF5b+oDZv3nzs2LGtW7fmZjh+/PgSr2U5ODhIH52xqtiKw83N\nTXr4+fPnuTnEx8ezA7Ozs52dnbnhrq6u3t7e+vr63JDdu3dXOmdGqhUH1+KCYRjpL/5//fUX\nN5w7AcW24qjlhmVkd6OK9NfeNWvWsAPl8catWrWKG/jq1asKCi7RioNhmGvXrknPc+XKleyU\nVWzFkZKSwl0u9vb2ln7vtLS07t27x03J3XDk5OQ0ZcqUqKgohmEuXrwovfS6deuWWM3yblQp\nsV5V3Kos2TazA6Cnp8fdrlXmVqrWalZrXWpABQOaYZhr1665urqW9w45OjpKRwbDMEFBQSVu\no2C1adMmIyODnYZr68pxcXHhLtNraWmxbajLy5FFixaVea1s1KhRRUVF7DR5eXllHrFy/bxA\npgHNMExoaGiZJzG0tbUXLVpU3p2EJRZam4Cu/YaVVUBLf+v/8ssvueEyf+NqE9C5ubnSDfwv\nX77MTlnFgB41ahT32uDgYPZtMjU1ZYd4eXkVFBSwUw4bNkx6Rbg2qdx1No6hoSHX7qWKAV3F\nrcqSbUBraWnt2rWLe0l5O1XVV7Na61IDqnaKg9WpU6cnT54cOHCgf//+Xl5eZmZmpqamXl5e\n/fv337179/Pnz3v27Ck9fb9+/SIiImbMmOHj42Nubm5ra/vRRx/t3r371q1b3MH1unXrNm/e\n3KxZM0NDw5YtW86aNSs0NNTf358dW1RUJN0bS2nLly+/evXqyJEjmzZtqq+v36BBg8GDB1+9\nevXnn3/m3l1dXd3Lly//73//GzZsWP369S0tLXv37n3kyBHpa+6y1bx58/v3769Zs+aTTz5x\ndnY2NjZu167dF198cffu3eXLl8v2emB5arlhZcXKyoprtrxnzx6uiaug3jg9Pb2WLVuyP2tq\nakp/1avU2bNnuebwgwYNYs+WWFhYcDfUhIWFrVixgv1527ZtY8aMsbW11dfXb9SoEfcpOH78\n+MqVK1u0aGFoaFinTp2BAwfeuXOHvYOmWqqyVWXIwsKiRYsWY8eO/ffff8ePH1/p9NVaTbmu\ni4ipzgVZQohMrFu3bu7cuenp6SUahhMiTTWPoAkRuOvXr1tYWFA6k4pRQBOiUDExMdOnTz91\n6tSsWbP4roUInaq1gyZE4A4fPvzrr7+uWbNmzpw5fNdChI7OQROiUBkZGcbGxoq5AEuUHQU0\nIYQIFJ2DJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKA\nJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKA\nJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKAJoQQgaKA\nJoQQgaKAJoQQgaKAJoQQgaKAJoQQgVK+gH737t3Tp0+LiopKj0pKSoqNjVV8SYQQIg/KFNAP\nHjzw8vKysbFp1KiRo6PjwYMHS0wwatQoBwcHXmojhBCZ0+K7gKp68eJFhw4dCgoKPv74Yx0d\nnYsXLwYEBGRnZ0+aNInv0gghRC6UJqAXLVqUn59/9uzZ3r17A0hMTPT29p49e3a3bt3c3d3l\nvfSwsLAyT6oQQlSAlpaWl5cX31WUhVES9evX79mzp/SQp0+f6uvr9+vXjxvSq1cveazRnTt3\n+H6XCCHydefOHZlHR+0pzRF0UlJSt27dpIc0bNhwzpw5y5cvv3btmo+Pj/wWXVBQACA/P19H\nR0d+SyGE8KKgoEBXV5f9mAuN0lwk9PLyunHjRomBX3/9taOj48SJE4W5cQkhpDaUJqB9fHwe\nP348derU/Px8bqChoeGOHTsiIiLGjBmTl5fHY3mEECJzIoZh+K6hSvLy8nr06HHt2jVjY+Mu\nXbqcPn2aG7VkyZLly5fb29sXFBQkJibKfI1u3LjRsWNHOsUhaBkZuH4doaGIikJmJgDo66Ne\nPXh5wccHNjZ810eEiz3FERwc7O3tzXctJSnNOWg9Pb2goKDVq1efPHkyKipKetSyZctcXV1X\nrlz59OlTvsoj/CgsxP/+hwMHcPEiCgvLnkYkQps2GD0ao0bBxESx9RFSK0pzBF0phmGio6Nf\nvHhR4lpi7dERtBAVFWHPHqxYgTdvPhhuawtra2hqIjERcXEoLn4/ytQU06djzhwYGyu4WCJk\nQj6CVppz0JUSiUTOzs4yT2ciRNevo3lzTJwoSWdLS0yejD//RFoa4uLw4AHu3cPr18jMxPXr\n+OYbuLgAQHo6li1Dw4Y4coTf8gmpItUJaKIWCgowZw66dEFEBADUr4+9exETg61b0asXTE0/\nmFhfHx074vvv8ewZzpxB27YAEB+PkSMxaBCSk3mon5DqUJpz0JVKS0vz9fUFEBoaWvVXMQxz\n48aN3NzcCqaJYLOA8C4mBoMH4/ZtADAwwJIlmDkTVTnvpKGBvn3Rpw+OHsWsWYiPx++/4949\nnDiBNm3kXTUhNaY656CTk5MtLS0BVGuNoqKiGjVqVFje9SUpWVlZhoaGNa+P1NKdO/j0U8TH\nA0DbtvjlFzRoUJP5pKTgq69w4gQA6Onh4EEMGybLOomyoXPQimBiYnL+/Pnz589X61UuLi4F\nBQUV3225Y8cOVDP3iYz99Rd8fSXpPGUKrl2rYToDqFMHx49j82ZoayMvD8OHY9MmGVZKiAyp\nzikObW1tukKomk6ehJ8fCgqgqYktWzBxogzmOXUqmjTB4MFIT8eMGcjKwjffyGC2hMiU6hxB\nE9UUFIRhw1BQAD09/O9/sklnVrduuHIFdesCwKJFWLlSZnMmREYooImAXbiAYcNQWAh9fZw6\nhf79ZTx/Ly9cuQI7OwBYuBBbt8p4/oTUDgU0EarQUAwciPx86Ojgt9/Qo4dcltKwIS5ehLU1\nAEyfjl9/lctSCKkRCmgiSG/e4JNPkJkJDQ388gt69ZLjstzd8ddfMDWFWIwxYxAcLMdlEVId\nynGRcOvWrYsXL67ixKmpqXIthshddjb690dcHABs3IihQ+W+xBYt8L//oU8f5OVh0CCEhMDZ\nWe4LJaQyyhHQvXr1evbs2c6dO/Pz842NjZ2cnPiuiMgNw+Dzz8HebTR1KqZNU9Byu3XDjh34\n/HO8e4cBA3DjBgwMFLRoQsqhHAHt5ua2adOmPn369OrVq0Rfo0TVrF8vORHcowc2blTooseO\nRXg4NmxAWBjGj8fhwwpdOiGlKNM56J49ezZs2JDvKog8XbuGBQsAwMUFgYHQ1FR0AWvW4OOP\nAeDIEfz0k6KXTsiHlCmgAbRp00ZbW5vvKoh8JCZi+HAUFUFPDydOoE4dHmrQ1MSRI3B0BIBZ\ns1Cdfl0IkTnlOMXB+eWXX/gugcgHe+o5NhYANm9Gixa8VWJlhaNH0bUr8vPh749792BkxFsx\nRL0p2RE0UVlbt+LMGQDw98f48TwX4+2N778HgMhIxV2lJKQUCmgiAI8f4+uvAcDZGTt28F0N\nAGDOHMnJ6P378dtvfFdD1BQFNOFbYSFGj0ZuLjQ1cehQyU73+aKhgQMHJOfBJ0yQdKRHiGJR\nQBO+/fAD7t0DgHnz0KkT39VIsbfH9u0AkJiICRP4roaoIwpowqsHD7BiBQB4eWHpUp6LKW3Y\nMAwfDgCnToEuUBOFo4Am/Ckqwuefo7AQ2trYv79KD69SvC1bJF2SzpiBhAS+qyHqhQKa8Gft\nWklD4/nz+WxXVzELC8kdK8nJ1KKDKJiStYOWuYyMjDVr1hQVFVUwzYMHDxRWjxqJjMSyZQDg\n4SH0p5kMHIihQ3H8OH79FSNH4tNP+S6IqAt1D+j8/PwXL14UFxdXME1SUhLomYSyxTCYMAF5\nedDQwJ490NXlu6DKbNmCCxeQkoLJk+HrC2NjvgsiakHdA9rKyiowMLDiaXbu3Hnv3j2RSKSY\nktTCwYO4dAkAJk9G+/Z8V1MFNjZYtw6ff46YGCxaRM+ZJYpB56CJwiUnY+5cALC3l9ywpxQC\nAtClCwBs2yZpF0iInFFAE4WbPx9JSQCwaRNMTPiupspEImzfDh0dFBdj4kSIxXwXRFQfBTRR\nrJs3sW8fAPTti8GD+a6mmho3xpw5AHDnDnbu5LsaovoooIkCFRdj8mSIxdDXx+bNfFdTI4sW\noX59yQ+JiXxXQ1QcBTRRoB073jd8dnHhu5oa0deXXCFMScHChXxXQ1QcBTRRlMREsE/+dXHB\nvHl8V1ML/fqhb18A2LcPd+7wXQ1RZRTQRFEWLQL7wPUff4SeHt/V1A67CmIxpk6lq4VEfiig\niULcv489ewCgTx/068d3NbXm5oZZswAgJAQ//8x3NURlUUAT+WMYTJsGsRg6OvjxR76rkZGF\nCyWPLpw/HxkZfFdDVBMFNJG/Y8cQHAwA06ejQQO+q5ERQ0OsXg0ACQn44Qe+qyGqiQKayFlO\njuRxVnXrYtEivquRKX9/yRMGNm3Cixd8V0NUEAU0kbO1a/H6NQD88IMy3TdYFSIRfvwRGhrI\nz5fcwEKITFFAE3mKicGaNQDQqhUCAnguRh5atcKYMQBw8iQuXOC7GqJqKKCJPC1YgJyc90ea\nKumHHyS9j86ahQr7rSWkulT0M0OEICQEhw8DwJAhwnoarGzZ2mLBAgB4+BB79/JdDVEpFNBE\nPhgGs2eDYaCrK2ntoMJmzoSTEwAsWUJN7ogMUUAT+fj11/dN69jehVSYnh5WrQKAhASsXMl3\nNUR1UEATOcjPl3zrt7YW+vMGZcXPDx06AMCPPyI6mu9qiIpQ90devX79ukePHoWFhRVMk5GR\nAXomYbVs2oSXLwFg2TJVa1pXHpEIGzeiQwfk5WH+fFT2HDVCqkKk5rlTWFgYGBiYl5dXwTRX\nr149fPhwZmamkZGRwgpTYomJaNAA6enw8EBYGDQ1+S5IgUaMQGAgRCLcuKEcz1okQEFBga6u\nbnBwsLe3N9+1lKTuR9Da2tqjR4+ueBqGYQ6zrRFIVSxdivR0AFi/Xr3SGcDKlfj9d+TlYfZs\nXL8OetAwqR06B01k6t9/sWsXAPTsiZ49+a5G4ZycMGMGANy4gRMn+K6GKD0KaCJTc+eiqAia\nmli/nu9SeLJgAaytAeDrr5Gfz3c1RLlRQBPZOX8eZ88CwLhx8PDguxqemJjgu+8A4OVLZX3u\nIhEMCmgiI2KxpMMgY2NJQqmtcePQpAkArFiBpCS+qyFKTOkD+t27d/fv38/Ozua7ELV34ADC\nwgBg/nzY2PBdDa+0tLBuHQCkpan73ypSO8oU0NHR0QEBATt27GB/vXv3bosWLWxsbFq1amVi\nYvLpp5/GxMTwW6H6ysqS9PVcrx5mzuS7GgHo3Rs9egDAzp148oTvaoiyUppmds+fP2/fvn1y\ncnLz5s0BPHv2rHPnznl5eT169HBxcfn3339Pnz599+7diIgIc3NzvotVP6tX4+1bAFixAvr6\nfFcjDGvX4sIFFBZi7lycPs13NUQ5MUpiyJAhIpFo9+7dYrGYYZjBgwdraGj8888/3ARHjx4F\nMGXKFJkvmj1mz8zMlPmcVcSbN4yBAQMwbdsyYjHf1QjJ+PEMwADM+fN8l0LKlZ+fDyA4OJjv\nQsqgNKc4rl271rZt23HjxolEIgAhISE9e/b8+OOPuQn8/Pw+/vjjS5cu8VejuuI6fd6wgW7N\n+MDy5dRVNKkNpQnonJwcV1dX7teCggI7O7sS09SvX//NmzeKrUvt3bkj6fR58GB07Mh3NQJj\nY4P58wHg4UPs3893NUT5KE1At27d+vLlyxn/dbbbtm3bO3fuMFIdiYjF4ps3bzJqO3QAACAA\nSURBVLJnqImCMAxmzlSXTp9rZuZM1KsHAIsWITOT72qIkqk8oA8ePJghgD7Ily5dmpSU1LNn\nz1u3bgFYvnx5VFTUN998U1xcDCAvL2/atGnh4eEDBgzgu1J1cvz4+06fXVz4rkaQ9PUlPUQn\nJGDFCr6rIcqm0rPUAPT09AYNGvTrr7/m5OTI/7R4uQIDA7W0tAA4Ojr6+Pi4uLgAsLS0bN26\ntYmJCYCAgAB5LJcuEpYtN5dxdmYAxtqaSUvjuxqhKCpiIiOZu3eZsDBGssuIxUz79gzA6Okx\nUVE810dKEfJFwsoDetu2bV26dNHQ0ABgZGT02WefnTlzpqCgQAHFlRYdHT1r1qwSZ5/19PR6\n9ep17tw5OS2UArpsK1ZImijs3Ml3KYJw8yYzciRjairZKgCjqcn4+DAHDzIF10MYkYgBmKFD\n+S6TlKTcAc16+/bt1q1buaSuU6fO+PHjL168WFxcLNf6ypOZmfnmzZuoqKj4+Hh510ABXYa4\nOMbYmAEYLy+mqIjvangWG8sMGvQ+l0v/c3dnLvf4QfLLlSt810s+oAoBzWGTunPnzmxS29ra\nTp8+/datW/IoTiAooMswZowkbi5e5LsUnp07x1haSjaGri7j78/s2cP8/Tfz66/M7NmMnZ1k\nlIYGs0R7hRgipkUL+pMmKCoV0AzDPHjwYOnSpfU/fBJow4YNT5w4IfP6hIACuqRbtyRf2AcN\n4rsUnu3dy2hpSSJ45EgmNrbkBPn5zPr1jKGhZJoROFwAbTopJChCDuiq3updVFR07dq1U6dO\nnTx5Mjo6mj12njBhwqBBgywsLA4fPrxr166hQ4fevn27devWNbxeWTtpaWm+vr4AQkNDq/XC\n8PDw/Ar77X39+nWtKlMxDIMZM8Aw0NPD2rV8V8OnnTsxcSIYBgYG2LsX/v5lTKOjg1mz0KcP\nBgzA06c4ghEF0AlcNE1r2DCYmSm8ZKJsKo3wEydOjBo1iuvgwtXVdc6cOTdu3BB/eFPv/fv3\nAcyfP19uf0sqkfRfv47VetXz589FVbv5LSMjQ06VK5kDByRHgwsX8l0KnwIDGQ0NBmDq1GGq\ncoYvOZlp106y5b7AHmbGDPnXSKpEuY+ghwwZAsDLy2v69OkDBw5s1qxZmZO5urpaWlpaWFhU\nJezkwcTE5Pz589V9laura0ZGRsVP9T5w4MCsWbOqmOMqLiNDcmucvT0WLuS7Gt4EByMgAGIx\nTE3x999o1aryl9Spg3Pn0K0b7t3DXnzhvmXB3HER6vtYA1I1lQf0unXrBg4c6FLZbQgmJiaJ\niYkyqqomtLW1u3XrVoMXVvqsbgMDgxpVpIq++w7x8QCwZg0MDfmuhh+xsRg8GPn50NHByZNV\nSmeWqSnOnkX7lgWv4nQWFH/f/LMF3UPXyLNSovQqv5Nw9uzZlaaz4mVkZMTGxr59+1YsFvNd\ni9p4/BhbtgBA584YPpzvavhRVAR/fyQkAMBPP6Fr1+q93MYGp/7UMdQuKIbmZw/mvN0ZJIca\niepQmr44WOHh4WPGjLG1tTU1NXVwcLCzs9PR0XFwcBgxYkQwe88xkZ8pU1BYCC0tbNmitr3W\nffstrl8HgC+/xBdf1GQOzZphx9YiAO9gPWaGOZOZJdMCiUpRpoCeOnVqs2bNfv75Z5FI1K5d\nuz59+vTp06dNmzYikSgwMLBTp07jx4/nu0bVdfQo2K5cJ05EOdchVN7165Iuoby8sGlTzefz\n2ZcGAR2fAfgnz2froIsyqo6oIr6vUlbVtm3bAPTs2fP+/fulx4aHh/v5+QFYv369zBdN7aCZ\n9HTJHRc2NkxqKt/V8CMri3F1ZQBGX5+JiKjt3DLSxfX14gDGEFkvzj2TRYGkhoTcikNpjqAP\nHz7s7u5+5syZFi1alB7r4eERGBjo4+Pz22+/Kb421bdkCeLiAGDNGrVtvbtwIV68AICVKyXP\n7K4NYxPRvi3ZIjDZMPzSP4MRM5W/hqgfpQno8PDw9u3bs73ZlUkkEvn4+ISHhyuyKrVw/z62\nbgWArl0xahTf1fDjxg3JNvDxwdSpspln13FuX3neAHAhteXPX9EVFFIGpQnopk2bhoSEFFf4\n3KCbN282bdpUYSWpheJiTJyI4mLo6GDbNvW8NlhYiK++glgMfX3s3QsN2X1oVv3RzE4zAcDc\nfY1TnqfIbL5EVShNQI8cOfLJkyf9+vV79OhR6bGRkZEjR468dOlS//79FV+bKvvpJ9y+DQBz\n5sjgi71y2rAB7BezxYvRoIEs52zqYLxx2ksAiWKLRf3CZDlrohJEDKM0J78mTpzIXq9zdHR0\ncnKqU6eOSCRKTU198+bNy5cvAQQEBOzbt0/mt/zt3LlzwoQJmZmZld7SompiYuDhgYwMuLri\n0SPo6/NdEA+io9GkCXJy4OGB0FBoa8t+ET2sQv9JaqGJ4ru7Q5uP46crG3VWUFCgq6sbHBzs\n7e3Ndy0lKc0RNIDt27eHhoYOHz48Nzf3+vXrQUFBp06dCg4OzsvLGz58+OXLl/fv3083ZMvS\npElgn3a2fbt6pjOAWbMkjyz/6Se5pDOAzcdstFFYDM3p0xjk5splGUQ5VbU3O4Fo3rz5kSNH\nAKSlpWVmZmpra1tbW2vI8KQg4Rw7htOnAWD0aHTvznc1/Dh3DmyzoM8+Q+fO8lpKo4/spna5\nt+FKq6u5bY4PPzz05Eh5LYkoG2WNNjMzM0dHx7p161I6y0VyMqZNAwBra2zYwHc1/CgsxPTp\nAGBqijVy7jNjyW/NrbVTAcw71TH/VvX6yyUqjNKNlGXaNLx7BwCbN4O/Hgr5tXkznj4FgCVL\nULeufJdlWkfzu69zALyC86ZBV1BQIN/lESVBAU1KOXkSR44AwIAB8PPjuxp+JCRg2TIAaNxY\nZg2fKzZ+qb2HdSKAFW/HJi36URGLJIJHAU0+lJSECRMAoE4dbN/OdzW8WbhQcn30xx/ldW2w\nBE1NrN1jDiAdpsvXG+D+fUUslQgbBTT50KRJks40t26V+xd7obp3DwcOAEC/fujRQ3HL7d1P\n6+P2WQB2iL98PnwxKnwSG1EHFNBEyuHDOH4cAAYNUtsen9lnLorF0NHh4fro2u1GGiKmADoL\nIwPwzTeKXjwRGCVrZidz2dnZ69aty62w8emDBw8UVg+fXr/GlCkAYGODHTv4roY3x45Jenye\nMQNubopeevPmGDkSh37BCQwJ2bixXd9L8PVVdBFEMNQ9oDMzM0NCQip+JmFsbCwAJbrlsiaK\nizFqFNLSIBJhzx5YWfFdED9ycvD11wBgY8Pb8evy70XHjzN5+aJ54lVXRo9EWBjq1OGnFMI7\nvvs7VQJq0R/0999Lnjg9YQLfpfBpyRLJZtizh88y5syRlBGEfsyQIXyWogaoP2gibDduYOlS\nAGjcGOvX81wMf6KjsXYtALRqhbFj+axk4UKYmwPAfKwqOnESu3bxWQ3hDwW02ktJwfDhKCqC\nnh4CA6HGjzCfMwe5uRCJsHmzLPsUrQFzc8kJlsdosh9jMWMGyurEkag8Cmj1xjAYMwavXwPA\nunXw8uK7IN6cP48TJwBg5EgIoVOzKVPg7AwA3+K77FwNDB2KzEyeayIKRwGt3lavxpkzADBk\nCCZP5rsa3hQWSroeMTaWPBaWd7q6WL4cAN7Cdh3m4OlT0DOR1Q8FtBq7eBGLFwOAmxv27OG7\nGj5t3Ih//wWAJUtgZ8d3Nf8ZMQKtWgHAOs2v38IWx47V6lniRAlRQKur6Gj4+aGoCAYGOHEC\npqZ8F8Sb6GhJtxseHpLu6wRCQ0Ny0TKrWH+x0UYAmDsXly/zWhRRKApotZSTgwEDkJQEALt2\nqfOpZwDTpiE7GyIRtm1TULcbVefri379AOBAzrAw3bYoLMSwYXj1iueyiKJQQKsf9sIge3vk\nzJkYqdbdw//2G4KCAGD0aHTpwnc1ZVm7FtraKBaLZrmeAoDERAwYgKwsvusiikABrX4WL5a0\nV+jRQ+4d0QtbWpqkK1FLS6xbx3c15XB3x6RJAHDxcd3fP90PAGFhGDECFT7hnqgGCmg1s28f\nfvgBANzdcewYtNT6Xv/ZsxEXBwAbNsDSku9qyrdkieSpCXPCA/J6DQCA06cxcya/VREFoIBW\nJ+fOSfp6trTE2bMwM+O7ID799Rf27weA3r0xahTf1VSoTh3JZcyoKKxrfRTNmgHAli3qfNun\nmqCAVhu3b2PIEBQWQl8fp07B1ZXvgviUkoJx48AwMDXFzp18V1MFX30luZS7coNu9M6/4OAA\nAPPm4fBhfgsjckUBrR4eP0afPsjKgqYmjhwRxK1yvJowAbGxAPDjj3B05LuaKtDUxNatEImQ\nk4Ppq2zxxx8wM4NYjLFjJQ9fJ6qIAloNPH+O7t2RnAyRCNu3Y8AAvgvi2d69kscSDBiAgACe\ni6m6Tp0wejQAnDqFU1GeCAqCvr6k4d2FC3xXR+SCAlrVRUXho48k18JWr6bbhcPDJXd129lh\n926+q6mmtWslXUNPnYrM5j44cQI6OsjLw6ef4soVvqsjskcBrdKeP0fXrnjzBgC+/RZz5/Jd\nEM8yMjBkCHJyoKmJw4cF3XKjTFZWkoaRb95g/nygTx8cOQItLeTkoG9fXLzId4FExiigVdfj\nx+jSRZLOixZJenxWY2IxPvsMT58CwNKl6NqV53pq5vPP8dFHALBjB65cAQYPxi+/QEsL2dn4\n5BP88QffBRJZooBWUSEh6NxZcmZj6VJJx2jq7euvJZfTPv0UCxfyXU1NiUTYtQuGhhCL8fnn\nyMoC/PwQGAhtbeTmYsAAHDnCd41EZtT6PgUAsbGxgwcPLioqqmCaxMREhdUjG2fOwN9f0sHE\n6tV0ZgPAtm2SewU9PHDoEM/98deSqytWr8aUKYiKwsyZ2L0bGDIEenoYNgy5uRg1CnFxmDOH\n7zKJDIgY1X4WamXy8/N/+eWX4grvmr169erhw4czMzONjIwUVljNbduG6dNRXAxNTezciS++\n4Lsg/gUG4rPPIBbDxgY3b6J+fb4LqjWGQffukrYbJ05g8GAAwJUr6N8f6ekAMGkSNm1S8ztF\nq6igoEBXVzc4ONhbgM1P+X4oohJQmofGFhQwEydKnjZqaMgEBfFdkCAcPcpoaTEAY2LC3LvH\ndzWy8+YNY2HBAIy5OfPq1X9DHz5kHBwk+0D37kxyMp8lKgl6aCyRv7dv0a0btm8HADs7XLki\n6adSve3di5EjUVQEQ0OcPo2WLfkuSHYcHLBnD0QipKZi6FDk5wMAPD1x65ZkPf/5B23aSLot\nJMqJAlolXLiAFi1w7RoAtG2LO3ckj+JQYwyDxYsxfjyKi2FkhDNn0Lkz3zXJ2oABkjbdd+5I\nPbDM3h7XrsHPDwCiouDtrXztvcl/KKCVXEEBFixAjx5ISACAL77AlSsCemoTT1JS8Omn+P57\nMAwsLHD+vLI2qqvU2rXo2BEA9u6Veh6WgQECA7F6NbS0kJuLL7/EsGFISeGvTFJDFNDKLCwM\n7dph1SqIxTA0xIED2LMHenp8l8Wzc+fg5SV5Fm6jRrh5E+3a8V2T3Ghr4/hxSddJs2dLHj4A\nACIR5s3DhQuwtweA48fh6UmtpJWOsgZ0RkZGbGzs27dvxWIx37XwITcXixe/P8PYsiXu3cOY\nMXyXxbPXrzF8OHr1QkwMAAwejJAQNGjAd1lyZmuLoCAYGqK4GMOHIzhYalznznjwQNL7Slwc\n+vbF6NFQumajakzJAjo8PHzMmDG2trampqYODg52dnY6OjoODg4jRowI/mDHVGmnT8PTE99/\nj8JCaGvj229x6xbc3fkui08vXmDKFDRsiKNHAcDEBHv24MQJmJjwXZlCtGghefoCe8v3nTtS\n4ywt8fvvOHBA0v33oUNo1Ajbt9MDWZQD381IqmHKlCkikQiAra1tu3bt+vTp06dPn/bt2zuw\nX/CAcePGyWO5Ampm9+AB06OHpBEVwLRuzYSG8l0TwzBMQQGTkiL5Fx///ueUFEYsluNyk5KY\nAweYHj0YDQ3JJhGJGD8/JiZGjgsVrJ9/lmwHMzPmxo1So2NimAED3u88zZoxf/3FQ5XCI+Rm\ndkrTjv2nn37aunVrz549V65c2aJFixJjIyIili9fvmfPnsaNG8+aNYuXCuXr6VMsW4ajR8Ge\n0jE3x/LlmDABmpryXvLbt4iJQWwsYmLw7h3i4pCUhORkpKYiLQ3Z2UhLq2QOIhHMzGBoCGNj\nmJnBzAzm5jA3h6Ul6tSBhYXkf3agmVm5d1cUFeHdO7x8iSdP8OABbt7EgwfvDwRFIvTujSVL\nVPmMc8VGjUJ+Pr76Cmlp6N4dv/6KPn2kRtvb4/ffcfo0pk/Hy5d4+BC9esHXF8uWoVMn3oom\nFeP7L0RVeXt7u7u7FxYWljeBWCz28fHp2LGjzBfN8xH0/fuMvz+jqSk58NHWZiZNYhITZb6c\n4mLm5Uvm3DlmyxZm6lSmTx+mUSNGT+/9IZfC/unpMebmjJMT4+Ii+efgwJiZlTu9lRUzbRoT\nESHzTaKUDhyQ7CyamsymTWVNkZvLrFjBmJi834K+vsxff8n3y46A0RG0DISHhw8cOFCr/FtX\nRSKRj4/Ptm3bFFmVHBUVISgIW7fi0iXJEA0N+Ptj6VKZXPYSiyVHUf/+i/BwPHmCJ0+Qm1vJ\nqzQ1YW0NKyvJYa+5OYyNYWAAY2PJYXKJNcjMBIDUVOTnIzMTGRlIT0daGlJTkZKClBSU2dFA\nXh7y8pCaWlElhoZo3hydO6NnT3TqpIAvEkpjzBiYm2PECGRnY/p03L6NHTvwQScFenpYsADj\nx2PVKvz0E3JzcekSLl1C06aYOhUjRkApujRQD0rTF0fHjh1TUlLCw8M1y/8sfvTRRwUFBdev\nX5ftonfu3DlhwgTF9cXx5AkOHsTBg3j7VjJEWxv+/liwAI0b13iuiYl4+BAPHyI8HA8f4vFj\n5OSUO7GhIdzc4OoKZ2c4OcHZGQ4OsLODjQ1EohqXUBLDIDkZKSmS/9lzJunpyMxEejrEYuTm\nIi8PurowMIC+PszNYWODevUktVEoV+D+fQwYIOlr1tUVBw6UcxojPh7r1mHXLsnfUgAmJvDz\nQ0AAOnSQ5ZstYNQXhwywh8a9e/d++PBh6bFPnz4dMWIEgDVr1sh80Qo6xREZyaxaxbRo8cG3\nd3NzZs4cJjq6ujPLzWXu3mUOHGBmz2a6d2dsbCo6pVCvHtOzJzNzJrNjB3PpEhMbK4/VI4r2\n7t37K8oaGsz48cy7d+VMmprKrF7NODl9sFvUr8/Mn8/cuaPypz6EfIpDaY6gAUycOJHNSkdH\nRycnpzp16ohEotTU1Ddv3rx8+RJAQEDAvn37RLL+sy/HI+icHFy/jnPn8McfePLk/XCRCN7e\nGDcOfn7Q1690NgUFiIzE48eIiEBEBMLD8fx5uc2oLC3RrBmaNkXTpvD0RJMm6tIWTQ0xDLZs\nwfz5kpNXJiaYNQvTp5c8GSVRXIw//8Tu3fjjD0h3wGtvj9690bMnfH1hYaGYyhVJyEfQyhTQ\nAB48eLBmzZp//vknKSmJHaKpqWltbd21a9evvvqqS5cu8liojAM6IQEhIbh5E9ev4/ZtFBR8\nMLZJE/j5YcQIuLlVMIPISMm/p0/x+DFevkR5PVrr6qJJE3h6wtMTzZrB0xO2tjJYCaJEXrzA\ntGnv7yI0NsbYsfjqKzRpUs4L3r3DsWM4dgw3b0L6RjANDTRrBh8fdOiA9u1VodtWABTQ8pCW\nlpaZmamtrW1tba0h597XaxXQOTmIjMSTJ3j0CA8fIjQUsbElp9HSQocO6NsX/fujUSNucFoa\n3rxBdDRevcLLl3j1ClFReP4cWVnlLk1DAy4uaNoUHh6Sw+SGDalPYAIAf/+Nb77B3bvvh7Rp\ngyFD0K9f+Zc24uIQFITTp3H5chmXLOrUQcuWaNYMHh7w8IC7ezlH5kJHAa3cqhrQz57h2TPE\nxSEm5n2gsjcdl6allde0dXLrnklNuyY4tX2XZZCYiLdvER+P2Fi8fYs3byoKYpaODtzc0KgR\nGjVC48Zo0gSNG1fljAhRX3/9hY0b8c8/H7SfcXREly5o3x4tW6JpUxgbl3pZfj6Cg3HpEq5c\nwZ07yMsre+6WlnBzg7MznJ3h6AhHR9jawtYW1tbQ1pbTGtUeBbRyq1JA79//5PM1cbATQyMV\n5kXQyoRxFoxyYJAFozSYZYmM0w3tMvRt0rQsU4pMUrJ1K2hEUZqeHpyd4eICV1e4uaFBAzRo\nAGdnOjomNfHiBQ4dwrFjH1z44Dg6wtUV9erByQnW1rCxgZUVzMxgYgJTU+hrFRo8DcW9e7hz\nB2FhiIj4ry/qCpmbf9A808QEJiYwM4OxMQwNYWAAExNoacHMDBoaMDUFABMTaGqW0X5T1oQc\n0Krz+U5LS/P19QUQGhparRfGxMQUlDgR/CHufHcF9pxzHI9/K5qCAbKACg+KdXVRty4cHGBr\nC3t7ySGIoyOcnGBrqyZNnogiuLpi6VIsXYrISPz5Jy5dQnAwuN38zRtJ+7xyaANtDQ3b6uhM\nFIlgZg8UFqKgQKOowFSUgfx8FBSgoKBkE/dUQKphuxGytFFYas7MfxMll71kDY0PGleWd3jy\n4dG6vnbR2gNW7p8oZadZqhPQxcXFD6r/8IgXL164lX85TlrFZ7pzOnTDsbJH6enByAgmJjA3\nh6np+3udLSxgYQErK1hawsoKdesq6Rk8osQaNkTDhpg+HQCio3H/Ph4/xtOniIrCq1dISCj3\n4nN2NrKzAbC9TGsD2oAhYC7fcsWAdOeVpROeVep+qyY/XFlFAc0vExOT8+fPV/dVrq6usbGx\neeWdUwMA3L9/f+jQoRXcxAhg6jRR6zbIyYGREbS1YWYGXV0YGkq+pREifE5OcHLCwIHvh4jF\nePcOSUlISkJamqTrlawsZGejoAB5eZLWe9wPnNJDylZcDLEYRUUoKgLDvP8fkPwvFkuai4rF\n79uTcAOl51P+qVojnYJxq6p0ECZAqhPQ2tra3bp1q8EL7Sp7/kh8fHylM2EbLhOiSjQ0ULcu\n6taV3xI0AU1AuNcPeaesAZ2RkZGZmamhoWFjYyPvZnaEEMILJYs26rCfEKI+lOkIeurUqdu2\nbWMYhu2w38LCAkBKSkpMTExgYGBgYOC4ceN2y+EBxjo6OgB0dXVlPmdCiECwH3OhUZqA5rHD\n/tatWz948KCovOvZ/+nUqdPkyZObN28u26VXXXx8/Ny5czdv3mxuLueL6eW7devWoUOH+O30\n9ddff42Ojp47dy6PNaxdu9bJyWnYsGE81jB58uRRo0a1b9+erwJSU1OnTZu2du3auvI8jV2x\nBw8ebNu2rdIeLrW0tLy8vBRTUvXw2VNTdfDYYX8VGRoanjlzhq+lMwzz9OlTALG8dkZ39OhR\nGxsbHgtgGGb+/Pm9evXit4ZevXrNnz+f3xpsbGyOHj3KYwGxsbEAnj59ymMNZ86cMTQ05LGA\nWlKac9Dh4eHt27evtMP+8PBwRVZFCCHyozQB3bRp05CQkOIKH0V88+bNpk2bKqwkQgiRK6UJ\n6JEjRz558qRfv36PHj0qPTYyMnLkyJGXLl3q37+/4msjhBB5UJqLhJMmTXr06NGOHTv+/PPP\nCjrsnzNnDt+VEkKIbChNQAPYvn37V199xXbYz12WZTvsHz58uPw67CeEEF4oU0ADaN68+ZEj\nR6DYDvsJIYQXShbQHDMzMzPq/I0QotLo2JMQQgSKApoQQgSKAlpmdHR0+L2dX0dHRyQS8V4D\n730aUA0CqYF2yNqjZxLKzKtXr+rVq8fvFcuoqCgXFxceCygqKoqNjXVycuKxhqysrJycHGtr\nax5rePfunYGBQU0eAy870dHR9vb2FT9oQt543yHFYvHr16+dnZ15rKE2KKAJIUSg6BQHIYQI\nFAU0IYQIFAU0IYQIFAU0IYQIFAU0IYQIFAU0IYQIFAU0IYQIFAU0IYQIFAU0IYQIFAU0IYQI\nFAU0IYQIFAU0IYQIFAU0IYQIFAU0IYQIFAU0kZfnz59v3bqV7yr4oc7rLkBZWVkHDx6MiYnh\nu5Bqo4CWpZcvX44YMaJBgwaGhoaenp7z5s1LT09XZAH5+fnffPNN586dTU1NXV1dR4wY8eLF\nC0UWIG3Lli2LFy9W8EK3b9/eqVMnMzOzTp06bd++XcFL5/Cy7iwh7AO8fxBKmDp1akBAQFhY\nGI811BBDZOTZs2eGhoZaWlofffTRhAkT2rVrB8DDwyM3N1cxBaSlpfn4+ABo0qTJuHHjevTo\nIRKJ9PX1Q0NDFVOAtL///ltXV9fMzEyRC50wYQIAd3f30aNHN2zYEMCUKVMUWQCLl3VnCWEf\n4P2DUMLx48fZrDtz5gwvBdQGBbTMDB48WCQSBQUFcUNmzpwJYMuWLYopYMGCBQAmT57MDTl7\n9qyGhoaXl5diCmCNHDnS3d2d/UgoMqRCQ0MB9OrVq7CwkGGYwsJCNp4ePXqksBr4WneOEPYB\n3j8I0mJiYurUqcM+e4wCWq3Z2Ni0atVKesjDhw8BjB07VjEFNGrUyNjYOC8vT3rgxx9/DCAh\nIUExNTAMM3DgwE8++eSTTz4xNjZWZEgNHz4cQFhYGDfk3r17AEaPHq2wGvhad44Q9gHePwgc\nsVj80Ucf1a9ff+HChUoa0Hw+UFKViMXixYsXl3hYakJCAgA3NzfF1KChodGlSxddXV3pgewj\njVNTUxX2ENXffvuN/cHT01ORl2X++ecfBweHZs2acUNatmxpa2v7999/K6wGvtadw/s+IIQP\nAmf9+vWXL1++cuVKcHCwghctM3z/hVBBOTk5sbGxf/zxR4MGDWxsbCIjI/mq5N27d3p6ejY2\nNuy3fgVr2rSpwo4iU1NTAXTs2LHEcPYEaEZGhmLK4Chy3SvG4z7A7wchNDRUR0dnwYIFDMOs\nWrUKdARNWLNmzdqxYwcAQ0PDq1evNmjQgJcyIiMj+/btm5eXt337di0t7T+4DgAABdRJREFU\nFX+jMzMzAVhYWJQYzg7JyMgwNjbmoSy+8bsP8PhByM3NHTlyZJMmTZYuXaqwhcqDin9u5SEn\nJ2f37t3cr25ubn379pWeYMKECb6+vs+fP9+5c6e3t/exY8f69++vyAKys7PXrFmzdu1ahmG2\nbt0aEBAgw6VXsQYF09bWBiASicocq6Ghds1JFbAPVEreH4QKzJ07Nyoq6u7du+zpHSXG9yG8\n8omPj5fegEOGDClvytjYWGNjY3t7e0UW8Mcff9SrVw/AJ5988uTJE9kuuoo1sBT5Nb+4uFhT\nU7Nz584lhrdv315TU7O4uFgxZXD4PcWhmH2g6uT0QSjP+fPnAWzcuJEborynOCigZeP58+c7\nduwo3aLL19cXQEpKimLKWLJkCQAPD48rV64oZokVUHBI2drauri4lBjo6OiosFyQxmNA87sP\nCOGDsG7dugoOSffs2aOAGmSFTnHIRkJCwoQJE6ZNm7Zp0ybp4YmJiUZGRqampgqo4eDBg8uW\nLfP39z948KDSf7Orvq5duwYGBkZGRrK3qACIiIh48+YN2/xOTfC+Dwjhg+Dl5cXessQJDQ0N\nCQnp3bu3k5NTo0aNFFCDzPD9F0JFFBQUWFtbm5qavnjxght49OhRAP3791dAAWKx2N3d3d7e\nnq/7tUpT8FHk5cuXAXz22Wfsr2Kx2M/PD8C1a9cUVgOHlyNoIewDvH8QyqS8pzjoCFo2tLW1\nt2zZ4u/v7+np2adPH2tr63///ffSpUs2Njbbtm1TQAHR0dFPnz61srIaOHBg6bGHDh2ytLRU\nQBk86tKlS0BAwIEDB+Li4tq3b3/9+vWrV69+8cUXnTp14rs0BRHCPsD7B0HV8P0XQqVcvHix\nV69eFhYWBgYGXl5es2bNUtjZ5wsXLlTwLsfExCimDGmKP4oUi8WrV6/29vY2MTHx9vZm2zDw\ngpcjaOHsAzx+EMqkvEfQIoZhZBz5hBBCZEHt2ocSQoiyoIAmhBCBooAmhBCBooAmhBCBooAm\nhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAm\nhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAm\nhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAm\nhBCBooAmhBCBooAmhBCBooAmhBCBooAmhBCBooAmBAAiIiJ0dXV9fX25IYWFhZ6enhYWFvHx\n8TwWRtQZBTQhAODh4bFw4cLLly/v37+fHbJ27drw8PDNmzfXrVuX39qI2hIxDMN3DYQIQkFB\nQatWreLi4p48eZKenu7p6dm9e/egoCC+6yLqiwKakPdCQkK8vb39/f3j4+NDQ0MjIiJsbW35\nLoqoLy2+CyBEQNq1azd9+vSNGzcC+PnnnymdCb/oCJqQDzx//rxBgwaGhoZxcXEmJiZ8l0PU\nGl0kJOQDs2fP1tHRyc7OXrBgAd+1EHVHAU3Ie4cPHw4KClq1atWQIUO2b99+48YNvisiao1O\ncRAikZCQ4OHh4ezsHBISkpCQ0LhxYwcHh9DQUB0dHb5LI2qKjqAJkZg0aVJaWtquXbs0NTXt\n7OxWrFjx+PHjVatW8V0XUV90BE0IABw7dszf33/27Nnr1q1jh4jF4g4dOoSFhYWGhjZu3Jjf\n8oh6ooAmhBCBolMchBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQ\nhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQ\nhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQ\nhBAiUBTQhBAiUBTQhBAiUBTQhBAiUBTQhBAiUP8HHsGwr42YH/UAAAAASUVORK5CYII=",
      "text/plain": [
       "Plot with title “Scaled normal: Red, Mixture: Blue”"
      ]
     },
     "metadata": {
      "image/png": {
       "height": 450,
       "width": 600
      }
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "M = max(M0)\n",
    "Mnm <-M*nm\n",
    "plot(xgrid, Mnm, lwd=2, type=\"l\",col='red',main='Scaled normal: Red, Mixture: Blue',xlab = 'x',ylab = 'y')\n",
    "lines(xgrid, mix, lwd=2, col='blue')"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "2d18d9ef",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "#### Reject and accept method\n",
    "\n",
    "-   **Theorem:** Let $Y \\sim f_Y(y)$ and $V \\sim f_v(v)$, where $f_Y$\n",
    "    and $f_V$ have common support with\n",
    "    $$M = sup_y f_Y(y)/f_V(y) < \\infty.$$ To generate a random variable\n",
    "    $Y\\sim f_Y$, we do the following steps\n",
    "\n",
    "    1.  Generate $U\\sim uniform(0,1)$ and $V\\sim f_V$ independently.\n",
    "\n",
    "    2.  If $$U < \\frac{1}{M} \\frac{f_Y(V)}{f_V(V)}$$ set $Y = V$;\n",
    "        otherwise, return to step 1."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 11,
   "id": "5e442acc",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeAAAAFoCAIAAAAAVb93AAAACXBIWXMAABJ0AAASdAHeZh94\nAAAgAElEQVR4nOydd1hURxfGX2DpYAEUESuoaCzYC1bsGhUblvhZo0YTe9fYYovd2HuLNZbY\nEzV2RVEUBUFRAhYQQUDpsAu75/vj3lyWZdkCCyw4v8fHZ3fumZkz9y7vzs6cmTEgIjAYDAZD\n/zAsbAcYDAaDoRwm0AwGg6GnMIFmMBgMPYUJNIPBYOgpTKAZDAZDT2ECzWAwGHoKE2gGg8HQ\nU5hAMxgMhp7CBJrBYDD0FCbQDAaDoacwgWYwGAw9hQk0g8Fg6ClMoBkMBkNPYQLNYDAYegoT\naAaDwdBTmEAzGAyGnsIEmsFgMPQUJtAMBoOhpzCBZjAYDD2FCTSDwWDoKUygGQwGQ09hAs1g\nMBh6ChNoBoPB0FOYQDMYDIaewgSawWAw9BQm0AwGg6GnMIFmMBgMPYUJNIPBYOgpTKAZDAZD\nT2ECzWAwGHoKE2gGg8HQU5hAMxgMhp7CBJrBYDD0FCbQDAaDoacwgWYwGAw9hQk0g8Fg6ClM\noBkMBkNPYQLNYDAYegoTaAaDwdBTiqdAp6ambty4sXv37rVq1bKwsHB0dGzVqtWoUaOePn2a\nr/Xu3LnTwMDAwMDA2tpaV2VeuXLF4D9iY2NVWB48eFCwHDNmTHYDd3d37mr16tV15V5Bkvfb\nGxUVZZAzFhYW9evXnzt3bkpKiq581vzxKWXr1q3yHhoaGn758kXBpkyZMvI2I0eO5NLz49Oo\n5yQnJ+f0cB0cHFq2bLl06VKFh6vnd6kYCvSNGzecnJymTJny999/BwUFpaamRkREeHl57d+/\nv2HDhp6enhKJpLB9zHf27dvn7+9f2F4UMVJTU/38/FauXNm8efP09PTCdkcJRPTw4UP5lNDQ\n0JiYGJ1XJJPJev7H3bt3dV5+wRMZGXn//v2FCxe6uLi8e/eusN3RlOIm0GFhYQMHDoyMjOTe\nGhoa2tnZGRkZCQanTp2aOXNmIXlXcMhksmnTphW2F0WV58+f//bbb4XthXK8vb3l3z569Cg/\naiGii/8RERGRH1UUFuHh4QMHDpRKpYXtiEYUN4Fet24d16EQiUTbt29PTk6Ojo5OS0u7evVq\nzZo1OZtNmzYFBwcXqpsFwfXr1y9evFjYXugv8+bNy/iP9PT02NjYbdu2CVfPnz9fiL6p4MGD\nB/JvFTrU8owdO5ZrXVxcXP77pXdMmjRJeL6pqamBgYE9e/bkLj18+DC/Rzt1RXET6CdPnnAv\nhg4dOm7cODMzMwAikahTp04XL140MDDgrvr4+BSaiwXIjBkzMjIyCqVqmUxWKPVqjqGhodF/\niEQiGxub8ePHt23blrsaGBhYuO5lp1KlSgAePnxIREIiJ9Dly5eX/5nIYWBgIDRQq4qCg4Pl\n++nBwcEPHz5MSkrKveuFgfzzNTMz++abb/bu3StcLSoKUNwEOiwsjHshaLGAs7PzsmXLZsyY\nMWPGDFtbW/lLX758mT17docOHezs7BwcHNzd3Tds2KAwCpmenr5//353d/cqVaqYmZlVqlSp\nZcuWmzZt0vCD6+fnN3r06EaNGllZWVWrVm3gwIH379/Pbvbvv/8OGDCgTJkyZcuW7d2799mz\nZ7VovBzcjMerV6+2b9+u1jg9PX39+vUeHh5OTk4lS5Z0c3MbO3bs8+fPFcx++eUX+TnGM2fO\nNGjQwMXFBcDUqVO5S61bt/b392/ZsqVIJDI1Na1bt+7+/fsBiMXi5cuXt2vXrmTJktWqVRs1\natTHjx8VfMj17Q0ODv7lP169eqXxTVJC5cqVuRcKn58CfnxKadGiBYD4+PiXL19yKenp6VxP\nsEWLFtk/8Nmnvx4+fGhkZCQ8KcFyypQpwmTazp07582b16pVK+HqggULmjdvzn1jjRkzhjNz\nd3eXr2vv3r1curGxsZCo4gPDoeFd1eHzFbCxsVFxVatmcmjYFq2h4kX79u25dhkZGf3yyy/h\n4eFqs1y/fr18+fLZ74yLi0tUVBRnk5aW1rx5c6U3sG7duomJiZzZjh07uEQrKyv5KtavX29i\nYpI976xZs2QymWB28+bN7J8bT09P4XVMTIyKhhw4cECw/PXXX7kXNjY2nz9/5gzatWvHJVar\nVk3I5e/vX69evey+GRsbL1q0SN69xYsXC9kPHz7MKUKVKlWIaMqUKdylihUrlipVSqGotWvX\nKnzQATg6OsbFxenk9sqP5Jw9e1bFLRImJwDMnz8/u4EgWy1atCjgx6eULVu2CNk3btzIvdiz\nZw939fHjx1zKmjVrRCIR93rEiBEqbtf06dOFAs+fP09Eb9++FVrXrl07mUzWv3//7I319vYm\notGjRwuW8n7u2bOHSxeJREKiig+M5neVtHm+8l/nU6ZMEdIzMjJev37du3dv7lKFChWSk5NV\n3CWtmqlVW7SluAn04cOHFe5R1apVBwwYsGLFisuXL6ekpCjYx8bGCn9UxsbGDRs2bNCggZC3\nc+fOnNmcOXOExJo1a7Zt29be3l5IWbhwIWem9GFfuXJFsHRzcxs5cmSTJk2ElLVr13Jm0dHR\n8oE+5cqVs7KyUmiL5gLt7e0tfBynTp3KGWQX6JSUFCcnJyFXpUqVmjRpYmpqKqTs27dPKF/4\ne7O3txd+gigINIelpaWFhQWyYWdnJ/92yZIleb+9pCOBjo+P37Vrl3B1//79Bfz4lCIv0A8e\nPOAGK0aPHs1d3bp1K3fp3r17Ggp0SkpKtWrVuPQ6depIpdLhw4dzby0sLP7991/OTH5k7Pjx\n40L23Al09g+MhneVI3cCnRNVqlR5/vy5kCXvAq1VW7SluAk0ES1YsCD7DxAOc3PzPn36hISE\nCMYTJ07kLtnZ2QmP7fjx40KWFy9eEFGtWrW4twsWLBDyduvWjUvs2rUrl5L9YWdkZHzzzTdc\norwizJ8/X7CMjY0loqlTp3IplpaWXNcmPT199uzZ8v5rJdCvX7/m7oOxsfHr169JmUALbhga\nGu7du5dLjIiIaNy4sXBbhA648PcGwMTEZPz48bt37z569ChlFegFCxZIpdLk5OQJEyYIiZUq\nVQoKCiIif39/Qbn69OnDlZzr28uRO4FWwY8//ljwj08p8gIdEBBQv359ALVr1+auctpqbGyc\nkpKioUAT0e3bt4XxkJkzZxoa8uOc69evF2x0K9DI+oHR/K5y6FagFy5cKN+rzaNAa9sWbSmG\nAk1Er1+/Xrp0aZs2beQ7gwIWFhbc7zUiEsYc586dK19C586dq1WrVq1atWPHjslksuP/ER0d\nzRkkJCS0adOGy9u4cWMuMfvDDggI4FK4JQZC+QkJCcJf1LFjx4hI6H8JHUYO+R69VgJNcqrR\nu3dvUibQQmTLd999J1/U8+fPhb/hP//8k0uU/3sTEjkEgS5TpoxUKuUSQ0NDBfuNGzcKxt99\n9x2X2KpVKyLKy+3VFk0EWv7PrCAfn1IUBPrHH38EYGBgwI0OcY+Puz+aCzQR/fTTTwqtbtas\nmfDgKB8EWv4Do/ld1RYNJ4SGDh0qZMmjQOdfWziK2yQhR/Xq1efPn3/79u2kpCQ/P799+/YN\nGzasRIkS3NWUlBTuA5qWlvb+/XsuUZADjitXrgQHBwcHBw8aNMjAwGDgwIH9+vWrUKHC9u3b\nBwwYUL9+/TJlyty5c0etJ0FBQdwLmUxWunRpYSqmRIkSwt9AUFDQhw8fEhMTubd9+/aVL2Hw\n4MG5vg8LFy7kflqePXv25s2bClclEsm///6rtNI6deoIqw2FKSkBa2vrPn36KK2xUqVKQo9M\nuOEAhJ/VCukA8nJ784Nly5YJff/CfXzZ4eYJiejRo0fx8fHcjBmXqBUrV64UuiYATExM9u3b\nJzw4naPwgdHwruaxUvkwu/T09PDw8FWrVnGXDh06tG/fvjyWz5HfbSmeAi0gEonq1as3cuTI\ngwcPvn37VpiJevLkSVJS0vv37+m/iKWyZcuqKOfZs2eurq6tWrVauHDhqVOnkpOTe/fuLfwG\nV4Ema5Y+f/4sPzft6Ogof7Vq1apqS8iJUqVKLVq0iHs9ffp0heD8Dx8+CJ8hhUoBVKhQgXsh\n3xHmUHGvsscScKiO9Mr17c0L8j1lqVQaEhLSuXNn7tLWrVu5J1K4jy87bm5u3IsHDx74+Phw\nn96c5ldVYGVlxXXGOb799lvhd3p+oPCB0fCu5rFShTBKR0fHWbNmeXh4cFeFjnMeye+2iHKd\nUw/58OHDuHHjuNfTp08XftFzlC5deurUqQMHDuTeRkVFOTg4CFdV7JMgFov79evH6dSgQYN+\n++03bgpr3rx5f//9t2qXKlasyL0oVapUTstGHBwc5Ffrfvz4UX4yTeia5Y7x48dv27YtKCjo\n6dOnCkPzjo6OIpGI0+jsq8U+fPig0ASBnFQ4d+Tl9uoKQ0NDJyenJUuWXL16lUsJDAx0cXEp\n9MengJOTk729fVRUlLe3t/Cdl4sedGxs7Lp164S358+ff/ToUdOmTTUvgeRisdWi8IHR8K5q\nXr7mfPPNN+fOnQPw+vVrTezVNjO/21KsBNrBweHevXvcuikrKysFgYZclLSVlVXVqlUNDQ3L\nly/PadPdu3c7deokWPbq1evNmzcAFi9eXLFiRaEXuWTJEiHAIHukcHaEqM+EhIT69etbWloK\nl6Kjo7nVHNbW1qVLlxbSz5w5U7duXeHtpUuXNGp8DohEorVr1/bo0QOAQmS3iYmJs7Mz1/s7\nc+aM/G/zFy9eCIsta9eunRcH1OLn55fr26tb5ENHuD2JCv3xZadFixZnz54VBLps2bK56KRP\nnDjx06dPwlupVDpy5EhfX1+lczbyCN8KCh0ahah21Wh4VzUvUHOE0Ybs3Q55NG9mfrelWA1x\nGBoaCqJ8/Pjxn376SRhiTk1NPXDggPB7v2nTptyIm/CrdsuWLcLqz2PHjl24cCEgICAgIKBh\nw4YJCQlCFULw+cWLFzX526tVqxb39yOTyRYuXCikHzhwoGzZsuXKlStfvvy7d+9Kly4tjPmu\nWbOGC9whok2bNp0+fTpXNyOTb7/9tmPHjkovCaJ89OjR33//nXsdGRk5YsQI7rNVqlQpYXFd\nPpGX28uhq4UM8l9gycnJyLfH5+XlJTgcHx+vlZPcKMeXL1+4zn4uus/nzp07duwY93rdunVc\nAO+LFy+WLFmi1J67FRzCyHVgYCDXFQVw/fp1+f64WjS8q0K6Tp5vdHT0hg0bhKVD8pFw2dG8\nmdq2RWtyPb2on7x7965MmTLyDbSysrK3t5efALG2tg4MDOTsIyIihO83Y2Pjpk2bChFmADw9\nPYkoMjJSPrurq2vdunXlf7XVqVOHK03pjLD8n2j9+vVHjhzZuHFjocAxY8Yo5OWoUKGCfL+M\nQ9soDgF/f3/5UWAhiiM5OblKlSpCurOzs5ubm7m5uZCye/duoRD5dQcKVQtRHELEBRHJ//C/\nfPmykC4MQ3FRHHm8vaS7hSryP3tXr17NJebH41u5cqWQ+PbtWxUOK0RxEJHC3nK//vorZ6lh\nFMfnz5/LlSvHpbu5uck/O5FI9OTJE8FSWHBUuXLlCRMmhIaGEtGNGzfkay9XrpxCM3NaqKLQ\nLg3vKoduw+wAmJmZ+fn5qbhLWjVTq7ZoS3ETaCK6e/eus7NzTs+mYsWK8mJBROfPn1dYQMHR\npEmThIQEzkaIVxNwcnISJuhFIhEXQ52TgsyfP1/pLNnQoUMzMjI4m7S0NKV9VWGHF+RBoIlo\n7NixwlX5P5inT58qHcQwNjaeP39+TisJFQrPi0Dn/fbqSqDlf/WPHTtWSNf548uLQKempsrP\nJdy6dYuz1FCghw4dKuT18vLiHlPJkiW5FFdXV4lEwlkOGDBAviHCJ0qYZxOwtLQU4l40FGgN\n7yqHbgVaJBLt2rVLyJLTh0rzZmrVFm0phgJNROnp6QcOHPDw8HB1dS1VqlTJkiVdXV09PDx2\n794tFouz20dFRU2ZMqV169alS5d2cHBo37797t275cNCpVLppk2b6tWrZ2lp2bBhw2nTpsXH\nxwu/ffDfulIVkadeXl5DhgypU6eOubl59erV+/Xrd+fOneyenD59esCAAVWrVrWzs+vWrdvR\no0flJ8ryItBRUVFCfJvCH4xYLF69enWPHj2qVKlibW3drFmz77//XuhiCOSfQOfx9upwqbcQ\ntmxoaCi/3ky3jy8vAk1EzZo141KMjIySkpK4RE0EWv5G9e3bV6hlxYoVQvrixYu5xOjo6OHD\nhzs4OJibm9esWVP40SmRSH799dcGDRpYWlra2Nj06dPnxYsXapd6K22dhndVJwJta2vboEGD\nkSNHBgcHy2fJ6UOleTO1aou2GJA2s7EMBkNXrF27dubMmfHx8QqB4QyGQLGaJGQwihD37t2z\ntbVl6sxQARNoBqOgCQ8Pnzx58rlz59ipNwzVFKs4aAajSHDkyJETJ06sXr16xowZhe0LQ69h\nY9AMRkGTkJBgbW2t2wWZjGIJE2gGg8HQU9gYNIPBYOgpTKAZDAZDT2ECzWAwGHoKE2gGg8HQ\nU5hAMxgMhp7CBJrBYDD0FCbQDAaDoacwgWYwGAw9hQk0g8Fg6ClMoBkMBkNPYQLNYDAYegoT\naAaDwdBTmEAzGAyGnsIEmsFgMPQUJtAMBoOhpzCBZjAYDD2FCTSDwWDoKUygGQwGQ09hAs1g\nMBh6ChNoBoPB0FOYQDMYDIaewgSawWAw9BQm0AwGg6GnMIFmMBgMPYUJNIPBYOgpTKAZDAZD\nT2ECzWAwGHoKE2gGg8HQU5hAMxgMhp7CBJrBYDD0lKIn0J8+fXr16lVGRkb2SzExMR8+fCh4\nlxgMBiM/KEoC/ezZM1dXV3t7+5o1a1asWPHgwYMKBkOHDq1QoUKh+MZgMBg6R1TYDmhKSEhI\nixYtJBJJx44dTUxMbty4MWLEiOTk5B9//LGwXWMwGIx8ocgI9Pz588Vi8aVLl7p16wYgOjra\nzc1t+vTpHTp0cHFxye/a/fz8lA6qMBiMYoBIJHJ1dS1sL5RBRYSqVat26dJFPuXVq1fm5uY9\ne/YUUrp27ZofLfLx8Snsp8RgMPIXHx8fnUtH3ikyPeiYmJgOHTrIp9SoUWPGjBlLly69e/du\n69at869qiUQCQCwWm5iY5F8tDAajUJBIJKamptyfub5RZCYJXV1d79+/r5A4e/bsihUrjh8/\nXj9vLoPBYOSFIiPQrVu3fvHixcSJE8VisZBoaWm5Y8eOwMDA4cOHp6WlFaJ7DAaDoXMMiKiw\nfdCItLS0zp07371719raum3bthcuXBAuLVy4cOnSpY6OjhKJJDo6Wuctun//fsuWLdkQh16T\nkIB79/D0KUJDkZgIAObmqFQJrq5o3Rr29oXtH0N/4YY4vLy83NzcCtsXRYrMGLSZmdn58+dX\nrVp19uzZ0NBQ+UtLlixxdnb+9ddfX716VVjuMQqH9HScPo0DB3DjBtLTldsYGKBJEwwbhqFD\nUaJEwfrHYOSJItODVgsRvXv3LiQkRGEuMe+wHrQ+kpGBPXuwYgXCwrKkOzjAzg6BgZDJYGgI\nmSzzUsmSmDwZM2bA2rqAnWXoM/rcgy4yY9BqMTAwqFKlis7VmaGP3LuH+vUxfjyvznZ2+Okn\n/P034uIQEQF/f9y4ASMjyGQ4fBg//wwnJwCIj8eSJahRA0ePFq77DIaGFB+BZnwVSCSYMQNt\n2yIwEACqVsXevQgPx5Yt6NoVJUvyZm3aoGdPtG+P/v2xbBmCg3HxIpo2BYDISAwZgr59ERtb\naK1gMDSjyIxBqyUuLs7d3R3A06dPNc9FRPfv309NTVVhE8hpAaPQCQ9Hv3549AgALCywcCGm\nTsXt2+jVC7/8gubNMy0NDHDmTOZbQ0N8+y26d8fx45g2DZGROHMGT57g1Ck0aVLQrWAwNKb4\nCLRUKn327Jm2ud68eePu7p6e0/ySHOnp6WwMujDx8UGvXoiMBICmTbFmDYYPx8uXEItx9Sqc\nnLIItDxSKRITUaoUfvgB587hzz/x2284dQrv36NNGxw8iAEDCrIdDIbmFJ8hjhIlSly7du3a\ntWta5XJycpJIJKpXW+7YsQNAsZlNLZJcvgx3d16dJ0zA3btIS8Pbt7hyBT//jNmzMXs2ANy9\nC09PKHxPt20Le3s8fQovL3z6hIgI/PEHypUDgLQ0DB6MjRsLvD0MhkYUnx60sbExmyEsnpw9\ni4EDIZHA0BAdOmDxYpiYoGNHnD4NFxfUro2VK3nLrVtx6hRsbbFjR2b2uDhIJEhKwoULePEC\n3bpBJgP3Y8jKCklJmDIFSUn4+edCaBqDoZLiI9CM4sn58xgwAOnpMDODgwP++Qe//46pU2Fo\nCDc3xYm+WbNQujSmTMmSeP8+IiNRowYAPpwDgJ8fvnxBQgK6dkVkJObPh6Eh5s4tkCYxGJrC\nBJqhx1y/zquzuTnOnkVUFE6eRN++AJCRgaZNERYGX180aMDbN2yI7dsVCylRQsn6lFKlUKoU\nANy+DXd3RERg3jxYW2PChHxtEIOhFUygGfrK06fo0wdiMUxM8Oef6NwZAIYO5a8aGaFsWXz5\nkhlalztq1MCNG2jTBp8+YfJklC3L5gwZ+kPxmSRkFCvCwtCjBxITYWiIw4fRtauigYEBHj5E\nZGTmqIVadu3CgQOQybBrF27fzkx3ccHlyyhZEjIZhg+Hl5dumsBg5Jmi0YPesmXLggULNDT+\n8uVLvjrDyHeSk+HhgYgIANiwAZ6eys2MjGBpqaYoX1+MHImxY9G9O374AQDMzfHDD7C2Rmws\njI15swYNcPo0undHWhr69sXDh6hSRUeNYTByT9EQ6K5duwYHB+/cuVMsFltbW1euXLmwPWLk\nG0QYNQrcaqOJEzFpkirjd+9QqpSqUY6bN+Hvj2PHMH48vvsOZmbo1AnNm6Nx40x15ujQATt2\nYNQofPqE3r1x/z4sLHTRHgYjD+T3kS065PLlywB69OhRwPVycdCJiYkFXO9Xypo1BBBAnTtT\nRoYqy6AgAqhSJVIRyR4fTxs30suXqsoRi8nXl6RSIqJp0/jaPTxy5T2j6MFtMe/l5VXYjiih\nKI1Bd+nSpQYXLMUorty9y8e6Va6M4cNhb49Nm3I0NjaGqSnMzWFgkKNNiRKYNAk1a6qqdMoU\nNGyI5csBYPVqWFkBwLlz2LYtN01gMHRHURJoAE2aNDFW+GXKKDZER2PwYHCnpzdsiKAgxMaq\nmrJzckJEBPz8IMrbSJ2tbeb/RkY4eJAPy5s2Ddrs68Jg6JyiMQYtcPjw4cJ2gZE/cEPPHz4A\ngKMjRo1Cu3aoWxfu7qpy2djooGouVq9RI/5t374oVw7t2kEsxqBBePKE71MzGAVOEetBM4ot\nq1fj4kUAGDQI4eHo0QNWVvD0hJ2dLmtJS8P587h6FfInWPr4ID4e8sfxuLlh2TIAeP1azSwl\ng5GfMIFm6AEvXmDhQgAwMsLSpflY0dq18PBAly78ikGZDIsWYfBgbNiALVtw7Fim5YwZ6NgR\nAPbvx59/5qNLDEbOMIFmFDbp6Rg2DBIJP9fXpAni43HuHB480K6cuDj1NrVqwcQEBgaoVAkA\nvL2xZAlmzUJkJHx8cPBgpqWhIQ4c4IdQxo3jN9JjMAoWJtCMwmb5cjx5AgCTJ8PKCubmePUK\nvXujY0fEx2tayD//wM4OgwcDwPz56N8f3CEM27dj/fpMs379kJKCxES+w96oEf73P8yfj2nT\nsHIlfvstS5mOjvzOHtHRGDcuj61kMHJDYcf5FQFYHHQ+8vQpGRsTQK6uJBZTQgKlpFBCAtWr\nRz168LHJmnDsGAHUvj2JxWRuTgBdv05RUXxQc2Bg7j0cPJgv5NCh3BfC0GP0OQ66iEVxMIoV\nGRkYNQrp6TA2xv79MDGBcGaNn592RQ0ahJo1Ub06TExw4ABCQtCuHQwNMXEiUlJQq5aSLBIJ\nYmPh4KCm5M2bcfMmIiMxZQo6dYK9vXaOMRh5gA1xMAqPNWv4QOM5czK3DM0dRKhShd+aY8AA\nzJ0LQ0MA2LQJe/YoX8nSti0qVFA/0m1ry69YiY1lER2MAuZr70EnJCSsXr06g1sckQO5OOqQ\noZ7Xr7FkCQDUrq3FaSYpKThxAv7+OHwYJ0+ibVs+vV8/XLiAf/5Bu3bKM757h9Kls2wMnZEB\nmQxSqfpK+/SBpydOnsSJExgyBL16aeotg5E3vnaBFovFISEhUpV/pTExMWBnEuoWIowbh7Q0\nGBpizx6Ymmqacc8eTJ6MUqUQFwdf30yBjo5GRgZu34aXF6ZNg7l5llyBgahTB05OePUKIhGu\nXYOFBe7exadPfDiHWjZvxvXr+PwZP/0Ed3dYW2vcVAYjDxT2IHgRgE0S6p79+/mZt4kTtcvo\n7U1OTjRvHp08SampmemJifT8OVWsSAAdPkyfPlHfvrRjB3/11SsyMaHatUkqpZAQAsjUlD59\n0q7qfft4nydN0i4jQ7/R50lCJtDqYQKtY2JiyM6OF7tbt3I0i4+nR49IJtOi5DVrqHNnioyk\nI0cIIAeHLJWKxUREKSnk6kpt21J6uqqinj6liRPp/fvMFJmM2rYlgIyM6PFjLbxi6Df6LNBs\nkpBR4MyZg5gY/rWKwY0BA9C0aZbFI2qZMQNXrsDeHj17YtYs7N6decnWlg8RMTfHs2e4dUvN\nFkuDB2Pz5swTtgAYGGD7dpiYQCrF+PGQybRwjMHIFUygGQXLgwfYtw8AunbFu3do3jxHS0dH\nGBtrFNYWGIg5c/D2bWaKtTVWrcK33+L0aQwZwu/BpAlTp2LqVABwcQGA6tWzXK1VCzNmAICP\nD3bu1LRMBiPXFHYXvgjAhjh0RkYGNWhAAJmbk7e3qo32ORIS+BcyGZ05Q/7+ys0GDCCAfvxR\nySWuuvXrNXLv3Tt+4CU4mDIy6NkzJStlUlKoalUCyMZG61Fshl7ChjgYDADAjh184POQIXBz\nU7OVKJAZLHH7Nvr0QYcOilFx27ejd2/06YPOnTF8uJISli3D+PEYMkQj9ypVwqEYhgkAACAA\nSURBVKpVWL0a1arByAiurnwwtTzm5ti4EQA+f8a8eRoVy2DkFibQjIIiOhrcyb9OThgwADIZ\nxGLcuoXTp5Xbv3mD+/f519Wro2pVdOoEI6MsNqtX49w5pKbizBn4++PlS8VCunfHtm0oW1ZT\nJ2fNwsyZamx69sS33wLAvn3w8dG0ZAZDe5hAMwqK+fPBHbj+22/o1AkTJ8LfH126oH9/vlst\nk2XujiSVolUrtGzJr/RzdERoKI4cUSxz2zbMnQtPTxw6hDFj8L//5W8TLlyAszMOH8Zvv8HM\nDDIZJk5ks4WM/IMJNKNA8PXFnj0A0L07evYEgMhISCSoUQNNm/JzcZ06oWxZPH4MAEZGqFkT\ntrYoXz7HMs+exaZN+O47WFmheXPUrIn+/flLZ85k9r7VkpiI168z316/jpIl+clABa5fR2go\nvv8es2dj2jQAePgQv/+uaUUMhrYU9iB4EYBNEuYVmYxatiSATEzo9Ws+JT6ebtzg5wn37aPj\nx6luXQLo2jU+V3Iybd1Kz5/nWGznzgTQ3LmK6c+eEUCWlplzjErx8aEzZ4j+m0i8fp1P79KF\nALK3V5IlOpqmTCGAqlShxER+XYy9PcXHq78JDH1FnycJmUCrhwl0XuH2AgVo5kwioidPqHRp\nGjeOv/rvvwSQoSG9fJllX9DduwmgevVyLNbHh2bNog8fFNPj48nVlfr0UbXIRSKh0qUJoHv3\nqE0bEonI25u/dOAAmZnR0qXKM8pkdO0avX1LRHT0KN+uWbNUNZ+h3+izQH/te3Ew8p2UFMye\nDQDlymH+fAB49QpfvuDhQ96gShX07g0rK7i4ZNl2rkUL1K2LwYNBBIlEyZKWuDjs3w8bG758\ngQkT8PEjjh9Xvokdh7ExOnRAQABq1MCNG4iL40/1BjB8OIYOVRK/wWFggA4dAGDzZhw5gkaN\n8OQJNm7E2LFwdtbsjjAYmsLGoBn5zJo1eP8eAJYv5zeT8/TEpUu4cAEANm7EN99g9mwcOqSo\np7Vrw98fc+agZUuULYs3bxRLfvIE0dG4c0cx/cEDfPrEDysHBGDjRiQkKNo8fozPnzFiBMqU\ngZFRpjpz5KTO8vz+Ox4+5HedFouVj1kzGHmksLvwRQA2xJF7wsLIwoIAatRI+fEoHToQQL/+\nmmMJ6elUvjwB9OiR4qXkZDpxgj5+VEwPCaG//uKr48a+16xRtClXjt9VI9fDx76+tG4dJSbS\niBH8QIcwes4oUrAhDsbXyoQJSEmBgQF++015t3TnTty4wZ8lqBSRCI8eISoKDRsqXrKwgKen\nkixOTnBy4l8PGoTUVHTurGjj6YljxzB5Mt+pl0rx6BHq1oWVFQBERqJcOTVNa9AADRrg6FGc\nPAlTU4jFmDYNvr6KkdoMRh5gQxyMfOPhQ5w7BwCOjmjVSrmNszPGjOFlUR4i+PoiKYnPnl2d\n1SKRwN4eq1bh3j3Uq6d4ddMmREfzY+IAdu+Gmxu/4HDRIjg4YM0ahIWpr8XfH8nJqFOHf713\nr9Z+Mhg5wwSakT8QYfp0ADA0xOrVfOLatbCwwOjR6rP/8QcaNYKHR+4dWL8enz4hPBzBwXzK\nvHlwdUVoqBJjBweIRPzm/dy3wtWrqFRJ8aiXxETs3p1lNHzBApw7h0uXULkyACxcqGS8m8HI\nLUygGfnDiRPw8gKAGTMyRzA2bEBqKv7+W312W1uIRGrGGW7ehI0NFi1SftXTE2ZmqFQps/vM\nnZUlRI/I4+GBuDiMH4/RozFwIAIC+C6/RJLFbPt2jB2b5QvG0hK9esHeHitXAkBUFH79VX3r\nGAwNKexB8CIAmyTUmrQ0fsu3smXpzBlydqZ9+4iITp2iLl3oyRONComLU54+fz7Nn09E9Ntv\nBFCnTpp65etLu3cr2UJPKuXjmn/6iQDq14+ISCajoCDFSGovL6penTZuVFK4TEYtWhBAZmZ8\naYwigj5PEhrQ133U3vv37zt37pyenq7CJiEhISYmJiEhwZqdRKchq1fzsck7duDtW6xciX79\ncOqUDkoOC+MHIoKDUbEi/v4bzZurn9BTzfffY98+7NmDRo0weTIMDbFjB78ftFY8fIgWLUCE\nQYNw7FieXGIUIBKJxNTU1MvLy83NrbB9UeRrj+JwcHCYN29eWlqaCps7d+4cOXLEQMWqB4Y8\n0dFYsQIAatfG6NF4+hR79qBUKVVZwsLQuTPc3bFtm5rCK1bE6NGQSlGtGgD07q3KOC0NMhks\nLNSUyW1hSoT69SES4cYNHD6MpUvV5MpOs2a8NP/xByZPVnUWAYOhIYXdhS8CsCEO7fjxRz4u\n+PJlIqKTJwkgZ2dVWS5eJIDKlVN/AmFsLJmYEEAzZqixTEujChWodGmKiSEi+vyZ2rZVviZb\nKqXQUPLxoX376NYtmjiRwsL4dH9/yshQU5E8b9+SmRkB5Oam3WmKjMJDn4c42CQhQ6e8fIld\nuwCgSxd06QIAvXvj6FFcvJjFbPJkVKqEwED+bdeuOHoUly+rWpzNUaIEfwiW2o2YJRIkJCA5\nGampvP3t29i+HRkZipaGhqhaFX37YtQoxMZi0yZUqACxGPPmoV497ZYIVq6MCRMA4P59nDyp\nRUYGQxlMoBk6ZeZMZGTAyAjr1vEpIhEGD0bNmlnMrl1DWBj8/QHA2xvt28PKCq6u6ssXiRAU\nhCNHcPgwrl7Fxo2KZ6wIWFvj5Uu8fo0KFQCgfXssWYKTJ3M8K7Z/f9SrhyZNAEAmQ/36fBNy\nWvadno6ePTFqVJbECxcyWzprFsRi9S1iMFRQ2F34IgAb4tCUf/7hBzd++EGN5evXdOIEpacT\nEc2YQQD16qVpLffv06JFFBPDb0d38aJGuf76iwDq1k0j4/R0fitRLjBj8GAlNgEBBJBIRFFR\nfMrLl3wUx6hR/H1YvVqzJjEKE30e4vjaJwkZOkMm40cDrK3xyy9qjKtXzzwwe/JkWFhg0CBN\nK5o0CY8fo0QJjB2LR4+g4cw719Hm/pfJQKRqTbZIBC8vnDyJVasAICwMYjHu3kWTJihZkrep\nXRu7dqF06czztCpVQo0acHDA9u3w9saLF1ixAiNHws5O06YxGAoU9jdEXomKinry5ElSUlL+\nVcF60Bqxdy/fbVy+XGdlennRmzeKiXv2UIcOFBysdWlv35JEQmIx1ahBlSur2c5/0SICqH17\nWr6cUlJo5UoCaMAAVVn8/Qmg0qUpOZnvsAM0YYLWfjIKFn3uQRelMeh3796NGDGCk0sAjx8/\nbtCggb29faNGjUqUKNGrV6/w8PDC9fDrJSmJ39eiUiVMnZqnory9MWgQfH3h44OWLdGiBSQS\nyMdBfv89rl1DtWp4+VJxpZ98IcIKb4HKlWFsjKQkhIUhIgJxcarcsLKCrS369cO8eTA3R7Vq\nMDPDN9/kaB8djXLl4OiIunVhZoZu3fgdmnbuRFCQRg1nMLJT2N8QmhIcHGxrawtgw4YNRPT6\n9Wtzc3MDA4POnTuPGzeubdu2ABwcHD5//qzzqlkPWj3z5/MdxsOH81rU0KEE0MiR9P492dhQ\nu3bUpg1ZW/NnZQkcOEAA9emTJfH9e/r8mZ4/J4BsbCg5WXkVL16Qvz+lpNDVq6T0scbF8dFy\n8gduZV+CKHDsGBkaUv/+WbZUPX+eDAwIoB491LWZUZiwHrQOmDt37ufPn3fv3j158mTurVgs\nvnr16pUrV7Zv337r1q3jx49//Phx4cKFhe3p10d4ONavB4CmTfHdd3kq6tMnVK6MPn0QHg5v\nb0RG4vp1vH2LxERER2exNDcHAEvLzJR37+DkhFq1YG0Ne3u4uCg5hIWjVi3UrYulS9G5M3/2\nqwIlSsDdHY0b86sWOYyNlVhKpfj0CcOHQyZDXFyWkI+gIHDLdC9exPXrGjWfwVCgsL8hNMXe\n3r5Zs2bC2woVKnTLNiPfsWPH2rVr67xq1oNWw//+RwAZGNC9e3ktavx4AqhZMwLI1ZVGjSJL\nS9q3jx4/VmL88WPmYpDYWLp5k0QiEono8GE+PkQ1+/eTqSmtX5+jwbx5ZGVFJ0/SgQMUGanE\nIDaWypenJk3IzIxsbfkVMQJRUTRhAn9eQb162i14YRQgrAetA1JSUpzlznyTSCTly5dXsKla\ntWqYJnv4MnSIjw+OHAGAfv3QsqVGWV6/Rp8+OH8+S6JEgtOn4erK7xA9aRLWr8dffyE5GVu3\nolEjJeWUK8cvbCFCy5Zwd4dUiowMzJuXY7CzPCNGIDFR1Yj5s2dISsL27RgxQnlHOzISEREI\nDkZQEEJCMs/NIsKlS4iLw+bN/Ial/v7Yv1+9SwyGAoX9DaEp7u7u5cuXj//vgKIePXrUq1dP\nJreaViqV1qlTp02bNjqvmvWgc0Qm48+UMjWlkBDlNmIxrVlDnTtndkKXLiWAatbkV1RzcEEg\njRtnyXvyJNWoQSdOqPekVSsyM6O5c6lFCzp7ViPnQ0OpVSvasIGIKCCA/vlH0SA6mv76i06f\npgoV+N34suPlRS9fZr7dvJmOHOHjwR0dSSajlBSqVIkAsrdXEzfCKCT0uQetXqAPHDgQn+tz\n23TH7du3TUxMmjdv/uDBAyJ6+vSplZXV3LlzMzIyiCg1NfWnn34CsF7FL9bcwgQ6R/74g58b\nVLrHBRGNG0dmZlSmTJb5w/BwcncngFq1yrT08aFy5bKUExRE9erRsmUaeSKV0sKFZGlJf/6p\n3CAmhnx8sqTs20cAVa9OEgnZ2RFADx5oVFdOcEtXjIzIx4ccHGjQID79yBH+Ls2Zk6fyGflD\n0RZoAGZmZn379j1x4kRKSkoB+JQTx44dE4lEACpWrNi6dWsnJycAdnZ2jRs3LlGiBIARI0bk\nR71MoJWTmkpVqvCbPgt7N8fF0a5dmcHLnBBPn07LlpH8h8fLi8qWpQULlBSbmEgPHpBUygto\nrVqa+uPpSUCOgl6/vuKyw6QkWrmSF+WuXaliRSXnzxJRfLzyAejspKdTv36yceNfv6bn50P9\nn2bwHxmZjJo35xcZhoZq2hxGQVG0BXrr1q1t27Y1NDQEYGVl9b///e/ixYsSFSFH+cm7d++m\nTZumMPpsZmbWtWvXK1eu5FOlTKCVs2IF3zFcty4zcdkyAqhLFyKi6GiKjaVbt0gqpeRkGjKE\n1q0jqZSOHlW1Z3///gTQpk2UkkLbtpGfnxo3rl2jv/8mIvr8mS5dorQ0JTYvX1KHDmRmpuRo\ncAGlm89JJOTgQMbGdOMGRUSoduTBAxoyhEqWpCE4TMBxDDQyotat6eBBktx7yIfceXqqaQ6j\nwCnaAs3x8ePHLVu2CEptY2MzZsyYGzduSOUDPwuQxMTEsLCw0NDQyMjI/PaBCbQSIiLI2poX\n6Lp1SSqlvn2pb1+6eZOqVaOtW/njThYu5O2vXiWAzM3p0iUCqEwZyumpTZ5MRkZ08qR6H6Ki\naO9eMjYmgP79l968Ua6h4eEkEpG1NX34QKtWUefOFB6uxEwsprt3SeE34ps3ZGDAa6udHeWw\nYPXDB+rbl78ZAH2HIwQcwyAhxcWFbnVezr+5fVt90xgFSHEQaAFOqdu0acMptYODw+TJk729\nvfPDOT2BCbQShg/n5cbUlDw8KCyMfyv8hOeWSk+aRGlp5OdHaWk0ezYdPkzh4fTNNzR2rKrC\nT50iTX4PcX3tqlWpRQt6+5ZMTKhkSSUHZX35QmXKkLMzpaaSoyM/1ODrq2j2yy8E0PffZ0l8\n+5aMjcnenkqWJBcXEouze3HlCj+Czf0bNIj27KE7h96e/EM6fTqVL8+nGxrSQuMVMhhQgwYs\n5E6vKFYCTUTPnj1bvHhx1apV5ccZatSocerUKZ37pw8wgVbE25vvVPbtm7la7+hROnYs00Yq\npWfPKCODBg0igLZs0bTw9+/5XeLkYzyUsm4d2drShQtERLGxVKoUVaqkfPVgWhofGT1zJhkZ\nEUDnzina7N1LRka0dKliemQkJSRQcrLS2Oq9e0kk4iV4yBASoqK4FCISi2ndOrK0zOxcS2BM\nO3eqaRqjANFngdb0TMKMjIy7d++eO3fu7Nmz79694/rOHh4effv2tbW1PXLkyK5du5KTkx89\netS4ceNcxfvllbi4OHd3dwBPnz7VKmNAQIBY5b69f/7554oVKxITE62srPLkYvGACG5u8PaG\nmRkCA+HkpMb+p5+wYwcOHdJ0kWF6Ojp0gIkJLl/WKJxZICUFRkY5rh7k8PTEqVMYPBhHjig5\nHODTp8yt6TRg506MHw8iWFhg717F/fgMDCD8bQUFoXdvvHoFAP1x6liZSaLXL9QcA8YoKPT5\nTEL1PehTp04NHTq0dOnSnL2zs/OMGTPu378vyzqp4uvrC2BO4QUSxcTEaNgief79918NDxtM\nYEGsHNwmGADNm6dplthY7ar480/atk2NTUIC9e6taRCewLt3tH07Kd2wxcuLTEzIw4PS0xVH\nopXBbb/B7fmheoSP+0gKYyAAfY89NGWKdp4z8g197kFrFGYHwNXVdfHixX45T6nHx8fb2dmt\nWbNGp+5pgUQiuXbt2rVr17TNmJiY+Fkl69evBxvi4IiPp3Ll+FUY+bTFa3Iyf+rg+PGqzLhZ\nRwsLfuThyRNq04byMsg2YAABVK0a1axJpUurCq3z8opp06eVsTdAJUtmrkIXhjWyvxZSGjX6\nbyt/ozkUEJB7bxm6o2gL9Nq1a0NyWiT2dcDGoDOZNo0XmCNH8rGW9u35pYYCv/xCU6dmiYST\nSGjJksxlKQsWEECdOuVYZnQ0DRhAe/bkaODhQQAtWkQ2NgTQ5ctUtiyNHJndMNlzOAEHMNzE\nhG7e1K5lkZFUpbwYICNkXK0/U7vMjPyhaAu0fhIfHx8eHh4REVEAcX5MoHkCA/mYtqZN6e+/\n6csXrUuIjaUTJ0jtwtTkZNq8mZ4+zczFfSsIKdn5+JEWLiR//xwNDh8mgMqVo9Gj6fx5JQaf\nP9OVKySRUFgYvXxJZ8/yHeqspKfTsAb+W/HjNwhUofYq8PMjS2MxQGURFbEj21wlo8BhAq0z\nnj9/PmzYsHLlyglDw0ZGRo6OjoMHD76X963UcoAJNA+3LFAkomrV+O3rDh3SroSxY/nYO9VI\nJIo7e6xaRXPnKl9LogkBAXT5Mk2bRj/8oOnqxIwMOneOBg3KDOUmIqJ58/gvC9WBggLyYx0C\nh3Ymc+mdzO7IEr76z1VhwwRaN0yYMIGb0HNwcGjWrFn37t27d+/evHnzCtyxzcDo0aPzo14m\n0EREx47xYjNxIo0YwQ8Tr11LRHTwIM2dq2o/e4G9e8nGRv3wCDfa8McfOnCbiJKTqWRJAsjf\nnyIiaPhwOnNGo4zPnvFNjo7mEu7e5YP0XF0pNVWjMnKatB7R8jVX9qaOrBNdyDCB1gFbt24F\n0KVLF9/sSwyIAgICBg4cCGCd/LJjHcEEmuLj+RUX9vb8yEZyMvn4kFRKMTF8TLQma/84wsOV\nhEmsXUtDh/Lp/foRQKdP08WLVKsWP/UnldJ33ykuJNEEmYzc3KhiRUFneTZtookTVX2veHvT\n1KlCPElSEjk788shAwMzrRQkWG0YEafLCfGyqmYRAFkiKeSK9ucrMnQHE2gd4Obm5uLikp7z\nRuwymax169YtW7bUedVMoGnyZF5XDh5UvBQZSSIRGRvThw8aFeXrS4aGVKdOlvGKjAyysiKA\n/vqLiEgq5VdjT5hAAP3vf0REISG8D+/f56YJCnMVaWlkakoAXb+u3P7ePQKoUiUh46RJfP2/\n/UYkJ8SaC7QQzsFxc3ewAWQAdSj9RCbN7egNI8/os0AXmQ37AwICmjdvLsp55YKBgUHr1q0D\nAgIK0quvAl9fbN4MAM2aYehQxav29nj7FuHhyHZ+gioUYs+NjLBtG2bNQseOAGBoCEdHAPj5\nZ2zejJUrAcDJCdu3Y/9+VKyYmfHMGcyfn+VI2ZwwzPpRNzXFmjWYOBGtWyu3L1sW1tZwduYy\n3r+PLVsAoHVrTJyYxX2FlV5qF34JBu1GV/uh7n0A1780/P0HL/VNYHyFFPY3hKa4ubnVrFkz\nQ+UmBu7u7qwHrWMyMqhpU77rOHmybsqMiMhxBFcqpdmzafNm9YXIZLR6Nb9hkyajK7NmkYOD\nkl35VfDfxngSCdWpww9uKBxdm0fiwhLKG0UCVMYwJjZYy+U8DB3BetA6YMiQIUFBQT179nz+\n/Hn2q69fvx4yZMjNmzc9PDwK3rfizLZtePQIAJo0wZw5uinTwUH5AawAfH2xahWmTEFcnJpC\nfH0xaxaSk9GrF9/vVs3Nm/j4EZ06YcMGTf38b9X4+vXgfpgtWIDq1QHAwID/l0dKVrDeMOkN\ngGiZ7fyefnktjlH8KOxvCC0YN24c53PFihVbtWrVq1cvDw+PNm3aCNs2jRgxQpbrSKyc+Xp7\n0GFhVKIEAeTsrMnqZyKiN29y3EdUYPp0srZWPvibnk7jxtGvv6qvSCym/v1p2jSNvCKi0FDq\n3j3LDqia8fYtf+4rkGVCUe1Ys1ozgU52vtzSlae7fdRbM3SNPvegi5JAE9HTp08HDx5sZ2cn\nfMEYGRk5ODgMHjz41q1b+VTp1yvQPXvyynT1qkb23BkoQ4eqMevQgQD1u23onIwM8vNT//2R\nFW6jZwMDTbdxVgh81kSgX17/YAwJQG3MH2n6RcjQHUygdc+XL1/ev3//8eNHtpIwvzh+nBeb\nYcNUmQmCcvo0deqkSqA/fqQ7d0gqpago+vtvjeKmC5vLl/l7oPZLJ49Ma/uYq+iEx2H11gyd\nwgS6aPM1CnRMDJUtSwCVLUsxMURE6el05UqWLYSePqXy5cnUlN/MjTu72to6yynX8nAbBWm7\nn9Ht23T5cu4akUkuVqUTSSTk4kLcjkhKTyuUJ4+DhXGxGWWNPwNUBW/SHiiJ9GfkH/os0EVm\nkpBRoEyahE+fAGDTJtjaAsCRI+jSBX37ZtocOoSICIjF+PgRABYuhJUVEhMRHAwA587hp5/w\n+XOmvYsLrKxQqRIAxMbi4sUs4XGHD+POHUU3Pn9Gp07o2hWvX2vhvEyG9etx/jz/dtculC6N\nBQu0KAEAsGkTv4PzwoWQ21wgXyhpY/TL7BQAb1FlY9/bkEjytz5GUaGwvyGKAF9dD/rMGf6H\nfe/emYn37pG1NU2YQDt30qZNREQhITRmDB08mLnkJDiYLl3iB3lr1iSAtm8nIoqK4vc5EoY1\nuNOqhN2cvb0JICsrxfNQpFJyd6fGjXMcmU1KouXLFef97twhgMzM+FxLl2qxd8Z/REby86O1\naulyMEb11CL3ryTiomeu0lmVDHXocw+aCbR6vi6Bjo4me3t+I3r5H/ZXr9LJkxQZyavIixdq\nyjl6lP73P4qKIpmMqlcnZD0sddkysrKis2f5t3Fx1KQJDR+unavbtvF75sv7c+AAOTtTkyY0\n87/NPDMy6PFjxeMER46k8uVzjGoOD9/S/rQp0gCNDkfUHNU9or/Op3OtmWS4WdXB5wydwgS6\naPN1CXS7drzkHT2amfjlC787UkAAjRtHI0ZoFwvh7k6Wllk2sKBsa685VqygNm3Un0bIMXcu\nAdS4Mc2alZnIRV106EAymaqzWZ2cCKD585VeTGjSnoAJ2Nyzp0aOcOjk52jH5okAmUAcXKO7\nsFKGka8wgS7afEUCzW2aDFCTJnT6NC1dyp9XIpORhwe1apXjUMPjx6rC0GQy5We5ZqdqVQLo\n9981MhaL6d49RRXbvZuf16tfnxwdczxt68ULfhXi3bvZnT1QcX407Nob3wnWZhcjpTuLaosw\n0OGJEzR9el6LY2iAPgu0NodyFkeSk5PXrl2bmpqqwubZs2cF5k9h8v49JkwAABMT7N6NNm2Q\nkICGDdG9OwwMcPZsjhnj49G6NVJT8eoVatTITA8KwsaNGDMGDRvCwkIjH37/HY8ewdNTMT01\nFVeuwM0NtrYwMuITTUzQsqWi5Xff4dUruLrixx+RmIiYGNjYAEBkJD58QKNGvFmtWujUCX5+\n/NJAOf74AyPClgJLZ01FtWpZLsmfA8stI5TfeUOz45fVQIRhQ+nG4Qh7RPluuN3w25twd9dB\nuYyiydcu0ImJiQ8fPkxPT1dh8+HDBwCkk78/vUUqxdChiIuDgQFOn4arK2bOhK8v2rRRn9fa\nGrVq4dUrXL2aRaC3bsWOHfj0CadPa+TDoUN4/hzLlsHEhE9ZsABHj+LMGVy+jNmzUbcugoOx\naRPGjAERRoxARgYOHcqyEZKFBdasAYDGjZGczPtDhFatEBKCv/7Cvn1wc8PUqUq9SknB7NkA\nYG+Pn3/WyGsoE2vNkRd9jqXLDDodmz9UeuCczKPhsGHw8+O/YxhfIYXdhS8CfBVDHMuW8T+t\nx43LTfZduwigGjWyJPr6Uv/+2ccQlJORwY85bNtGW7YQd7cbNiSAdu+mv/6iUqWoeXMC+POw\nP3zgHdZw+yJ3d7Kyoq1bCaASJRRHwLdsoSlTKD194UK+VK2Os9Jw2bfSq8IepPKWv/c88RI1\nv8XF8+hJ/ftr4QpDe/R5iIMJtHqKv0B7eZFIxMeUaThYrMCXLzRvntZHqCqwfj0NH86r8Pr1\nRESvXtGhQ/wos0xGSUl0+XKmh/v30+7dmhYuk1FKCqWm0rx5dPp0lkv/7Q0defS6uTkB1KiR\n8inMXPRntM3CKfXnz1S6NAH0DQLTIaKdO7WumKExTKCLNsVcoGNj+UWAZmb07BmfmJZGrq7U\nrFmeYoBXrKDevdUfEavAhg1Ur16mJ7lA2xq5SsePH9hXwm27kdOfasH84ORqWbuWF+tdGEPm\n5qrOw2XkDSbQRZviLNAyGfXowSvBli184oUL1Lo1AWRion6Nc05IpVSqFAGZwc5RUari3nTF\n8uUEaLSjdFb++Ye/Ddz5LfLkruOcRzVPS6MqVQggB0QkwZJcXCghIU8lMnJAnwWaLfX+ulm1\nChcvAkD//vjpJz5xzx7cvQtPT8yciYYNceqU+nKyz7IaGmLfPixejG7dyEnnOQAAIABJREFU\nAODWLTg44Ntv+avXruHnn5GQoL7kgwfRtSvUBtKkpSEmBgC/7jwyUo397t04dEje/UmTAMDa\nGqtWqXdKLURZ4j1ysXO0qSmWLgWAj3BYixl49QpjxujAM0bRorC/IYoAxbYHff06P/RcrRrF\nxWWm+/nR3LkUFkYjRxJAkyapKiQkhLp1IxMT+vlnVWZ//UUACefdcLsQcQvBOZKTacsWxZGN\n+Hj+GO2uXVUVLpVSzZpkbExBQSQW06NHarrq2Y43XLWKT1izRtFWJ9HNalE6WyiV8htMWRml\nRMCB8N95iAydos89aCbQ6imeAv32LdnZEUAWFjkO+H76RIcO0bFj5OpKFy8qt5kzR8nGHUp5\n9SpzncvPP1O9evT2bebVPXsIoNq1s2SRyahVK7KxoRs3VJWckUFOTmRoSAEBanzgkEpp4EAa\nPpx+/526dQu//a+lJV+5wpC7WnXWoXwrLefGDb6K762OE0DGxnmdiWVkgwl00aYYCnRyMr/W\nGaDD6jYgHj2aABo0iMaNU3IMSmAg9e9Pq1dn6YOrhav92LHMlKAgatCAVv23SVBGBn+wt4Yk\nJGi6QJwjOpquXaPGjQk48M0qbm4w+5EPmgh0fsOdmmBkKHtm2pQAKlOG3rzJ91q/JphAF22K\nm0DLZNSxI689Eyaotw8Lo3Xr6Oef+SXgOuGHH8jFhUJDlfjG0a8fAXw83PPnlNPNl0rp4EF6\n+FDTeqOiaPRoOnuWP1tgxoygvnNtEQMo7tRUMCMbmhAURMbGBFD7bz7ybrm65nhDGNrDBLpo\nU9wEmpNari+meRRdaCgNGkTnzyu5dOIEPXighQPx8WRlRUZG9Po13bmTuZv+tm1kbU2HDhER\n9epFAP3xB124QAA1b668KC72wsYmM245OlpV1du38wtqpkwhS8vEs9fKlyeA7OzU5Ms1OhH6\nyZP5cv7stZ9/1bNnQYTEfB0wgS7aFCuB3ruX/wt3ccndOSOKPHpEAFlbK1nh8ukTfxqLAmIx\nfw7roEEEUMeOfLqHBwHUpg0RkURCISFERLdvk0hEPXoorz0yklxdafRoevWKiGjDBgJyNCai\njx9p5Ej6808iovT0UaP4m6Hh7ky5Q+laQa2IjSVbWwLIyYlSu/bmy5o4UYdOfs3os0CzMLuv\niStXwJ2MbmeHS5dQqhSgLEJOK6pVQ7166N4d5uZ8yps3ePMGX76galU4O+PLl0zj9+9BBBMT\nfP89TE1Rty5MTTO3K2rRAgB/mIixMZycAKBNG0RHZx6PooC9PZ49g58fXFzwzz+4excA7t3L\n0dty5bBvH/r0AXD5mmj/fgDo1g1Dh+b+BqiFi7fLHnineeydjQ2WLAGA0FCsbXwc9eoBwObN\nWLdO594y9IvC/oYoAhSTHrS3N5mZEUDm5plL5V68oBIlVAVgSKXk66vFxsSxsWRhQWZm9OoV\nlShBNjZZRjAA+vFH/i23g35qambepCSaOJEuXFAsU+k4zLt3tGULPzDRvj2JRHTvHn34QH36\n0JkzFBFBEyeqCHiIjSVHRwKoZMkCiqKTf61hjfJmGRnk6soH3bx9EEEVKhBAhobq53gZ6tDn\nHjQTaPUUB4EODORHFZD12NYrV/hfzh4etHy5koybN/NjEdkRJvSI6NIlql+fzp+n5GRydCQH\nB4qPpy9fsqy63riRAPrhhxydvH+fH1CWP/3k2jUyN1cSi80Nj3AbJ2VkKI6lcIHNOU9penry\nN2P//rwuFNQke+7GNxSy3L1LBgYEkIcHkb8/v1DT2Fj5xABDY5hAF22KvEAHBxM3FwZQ5cpZ\nLslkdOcOv0+/paWSeacjR5QHewQEkK0tjRrFvx03jgAaNoyISCzme9ypqbRsWZYzo4KDFXch\nkkpp6lRat46IKCqKnJ0VN29bvJgAat9eiWO1avGFSySKG/P/+y/160dnzii9H1zItXzotrbq\nqVag5a+qKFxb4R4+nM9y9izRnTvE7e1kZkbXrmlRCiMrTKCLNkVboENCqGJF/s/azY0+fFBi\nIxbTL78ol7P0dOXxDX/+SQDVrMm/DQ+ntWsVI5E5Gzs7Ve49fsz79vmzkqtcB9/FJceDUTia\nNCFjY/LzU2XzH8+f878lypfPbJluRzkU5DuPPXR5Pn0iGxsCqGJFSkggunSJP4rMwkJJFDdD\nM5hAF22KsEAHB2eq86JFWmdPSaHKlalKFUpKUryUkUGXLmVZCpidqCjq0iVz7YlSMjJo8mS+\nB52de/dIJKLOnVWVIJPxC8e9vVWZERFRfDxvyy0g1+cpGAXfBG+F7j8/mH/qFL9e39JSyTIi\nhgYwgS7aFFWBDgzMHNkoUybHtdoq+PSJTE3JzCz3e9rlndhYVQfUnj9PK1ZQbCz9+6/akqRS\nflUeQEuX6rtAc2Tvictk1L49P0HId5qPH+c12siI9u4tLFeLLvos0CzMrpjy8CHatEFEBADU\nr68qUk0FZcrgr79Qpgx++SU3Pnz5wu8wp4LHj1GtGlauzNHAxibLiVbyyGQYNgzz5uH+fTg7\nq3Vn9mxcuAAAvXph3rwscW+6Qoic0zCETnWwnfwlwVsDA+zaBUtLyGQYNQpJScDAgTh2DAYG\nkEoxZgyOHs21/wx942s/k/DDhw/9+vXLyMhQYRMdHV1g/uiGixcxaBCSk2FggFWrMHgwTp/G\nwIFZbFJTMWwYypXD5s3KC/H3x/v3ABAWhgsXsH07Pn3C0KHo1AkzZmSxlMkQHQ17+yyJycmo\nVg1paQgNVbwkj7c3QkJw/jzmzNG0dYcOwccHK1fCwgJTp8LHR5ODE7duxdq1AFC7duYphtnP\nAywUcnIjJ9+cnbFqFSZMQGgopk7F7h1SfPstli3DokXIyMDQoYiIUHxGjKKJAenDJ7TwEIvF\nhw8flkqlKmzu3Llz5MiRxMREKyurAnMs92zdismTIZXCyAg7d+L775WbHT2KIUMA4OFDNG2q\neFUqhYMDoqNx/Tqio1G7NurUwcmTGDAA9vaKuy0PHIiTJ3H2LHr1ykxMTkblyhCLERKCsmVz\n9DYlBX/8gTZtNOkCAwARypRBbCxOnkT//hpl+fXX1LVbu8YdvyNrZW+PBw9QtWpm51T+45+X\ns191giYOcDYyGTp1wvXrMITsc6X6JePeITAQISHw8EB8PAD8+CM2boToa++BaYJEIjE1NfXy\n8nJzcytsX7JR2GMsRYAiMwYtkdD48fxoJUAdOqgyjomhKlWoZk1KSaG3b2nVKsUYDE9PqlqV\nIiIyU1JSaPlyJRFd3bsTsm5NxxEfryb6Infs3EmjRinfLUg+NPs/Iut0IGA61pYoQU+eZKZn\n/+wrHZVWSMzvkWvNCw8LI1tbMoH4k0FZAigwkIjI359fwwJQp075cv+LHfo8Bs0EWj1FQ6Aj\nIvhzqgD+wNGmTTXNy23MLwQ1a0taGgUF5TKvDomOpgoVqEMH+UnFPXuoqtG773DEzjLl9u3c\nlJo9miJ3heSHrJ85QwYG5IAIzzovMhd7hofzp6FzS5CePtV9xcULfRZoNklYLLh+HQ0a8DtR\nNG0Kf3/cusWfZaUJffuiUSMMGJDL2k1N4eKSy7ya8+oVli7lpz2VEh6O8HD4+kIsBkCEBQsw\nZgzeSCudt/ru5EVzhZFqYYJO9YSewoBD7gZAVExIar4jR/YZxd69MWkSPsLhZEAt4cAyODri\n7l1+yiE0FG5u2L07N04z9IHC/oYoAuh1D1ospjlzyNCQ7zF9/32W3S0E3ryhzp1p4kSlgwAF\nzbt3VLUq9e1LFy5o4Q+3OlthzfeVK9SwYeZa55s36cULIoqN/X979x4VRd3/Afy9LBcFuQmC\nCAgqBAioqSUiavg8eUGLfPRJwEt0siOPt06aPVrZ06lTodjjT0VR8zl5qdQ85+nEY+alQslL\ndBEvoEioKYggCShyW2C/vz92W+4IuszMyvt19nh0dmbnMzLz3i/fmflO/bNwnZzuc4W0vAdB\n+9fe4pwajRg1Sr+ljZ6HpdWKVav0l98BYvp0dne0RsktaAb0/Sk3oM+cEUOG6I9AGxuxfXur\ncy5bpp/t5MlW55k1S4SE3OfR0Wlp7bxhry265xPqvlTaf2/Fl1+K0FDR5CjS9bnHxDScdvBg\nfTesv7/Izn7YeiXW0S7v/D+HTlKrxVdfNX5v1676cxJ9+oivvzZ6tY8ABrTx3blzJy8vLz8/\nv66NuxiMRIkBXVEh3npL/6QNQAwdep9e4MxM4esrwsIajUPU5AN1d0C3MfT+9etCrRbdu4s9\ne8T777c8xN327SIxseXFq6vFgQOiqEjU1Yl9+8SkScLbu2PPqWouL0+sWiVOnBCbNoni4mvX\n9GMo6V7TpjUarKkhaVrND99h3c7O69Onhe6xitbW4vjxxu99+KF44on6/5TZs8WtWw9S1qOL\nAW0058+fnzNnTu/evQ1dNGq12t3dPTo6+njTHdNoFBfQycliwAD98WZhIf71rw48GKUN330n\nPv1UlJaKVavE6dMtzHDvnhgwQAweLFxcBCD27Ws6Q1GRvqqDB1tYPDFRAPe5b7sNx46Jzz5r\n+a2pUwVwaNgKK6v6IDLcEt1cJ52ya5KqbaylQwW0c+b9+/X9Gfb24qef/px65YoAhJ2dSErS\nj34HiJ49xaZNfCCLAQPaOBYuXKhSqQC4ubmNGDEiIiIiIiIiJCTEw8NDF9Zz587tjPUqKKDP\nnBHjxzcKgISElue8fl08/7z44osOr2L9en2TvEV1dUKrFe+/LyZObDjCp0YjSs9fL1+dqBkd\nLoC6/j7FxUL3qu9kPnJE2NqK5cs7XJIQoqpK2NoKoEn78I8/xPbt4qPA/1yE/1NIAYRKJWbM\nuE+itSfvOprgzWO0Pa3gdoZvO4vZuVPfb+Tg8GdXVnGxcHUVQUGiulrk5YnnnqvfcwYNavl7\ntOthQBvBxo0bAUyYMOF0S427jIyMGTNmAPiotWF3HoIiAjorS8TE1J8MdHTUj9++ZYsQQlRU\nNO0r0OVsUFCHV3ThgggNFZs3i40bdW3k/Hzx00/iyy/Fhg1i5Urx0ksiMlKEhYnAQOHuXt8s\n24VZAvgUM2+h13a80PBLRKUSjo7Cw0MEBdSOHCkmTRIxMWLBAvGvf4l168Snn4oDB0RamsjO\nFkVFoqamlcJmz9YOG37zYsnx42LbNrFwoRg2rH7MI91aIiLaM2KS3sOHuGjfVdJtt6aN6+OP\n9fuIjc2fHc4aTaPBTJKTRb9+9TWFh4sffpCiMgVjQBtBaGion59fTauHr9BqtaNHjx41apTR\nVy1zQJ8+LaKi6qPIwkLMny+KikRlZf0lrkOGCJWqUfdxYaFYtEgcPtzqx37xhf6Z2UKIQ4fE\nP/5Rd+Pm1avi0CGxYYOIjz4jgBqVhZvV7YZR28YrCrsvwn8ivlFB285FWnt16yYcHYWXl+jf\nX//y8Kj/Jmj+6tVLLF6sv1Gj/R4gMR84ZI0Y0Pf9nO3b9TuLWi3WrRNCoxGnTzfq0KisFB98\nIOzsGsX0wYOKuMJHDkoOaJO5EzQjI2Pq1Knmrd+6qlKpRo8erWtoPwpqa5GcjMREpKTop5iZ\nISoK77xT/xC/IUPq39K9DFxcsH59qx+em6u76vnQlt+rvzs+eV+sWtS+vc37/ZrXde9bImAg\nnskVnjerezZcTq2Giwtu3kR4OHr2hKMjbG1hbQ1bW6hUUakOUVOBqQ22QHdx7j//iepqlJXh\n7l3s24cnn0RJCYqLUVzc8tXBVVWoqmr0LMPmbGwwZAjGjMGECQgLg1rd1sytUchYHPfVoXvQ\nX3gBjo6IiUF5OV55BX5JyyZkrcNbb+G99/RzdOuGFSvw8suIj8emTaisREoKUlIQFIRFixAT\nA5MY0qBrMJmADgoKSktLq6urU7d+LJ46dSooKEjKqjpFVhZ27MCOHbh5Uz/FzAzPPosPPkBA\nQMuLnDyJkhI0OHfaXFERzp3DuXPIyEDG2T7vqiOq68z/Ns9jPU6qUZsDn5010YaZLWwsV/ok\nDxiAJd7w8oK3Nzw8MGwY6uqQnw+VCt9/365NWbCghVgxxKIQuH0bxcX6P0tKUFqKO3dQVoY7\nd6DVYutWAJg1C9bW6N4djo5wdUXfvvDxwYAB7QrlNqLtAaL5gdP8Ib8GGi7e9g0vuneffRap\nqXjuOeTm4mRWzwnAlTtO/Zss4OyMNWvw2mtYswZbt6KsDBkZmDcPy5ZhxgzExmLkyA7cRUOd\nRO4mfHvpmsaTJk06d+5c83cvXboUExMDYPXq1UZftURdHNnZIj5ePP54o9/eHR3FwIECHb4P\nu7JS/PKL2L5dLF0qnn5auLq22j/giOKFzrunjSt+9VWxebMAWn7oSnsY95SXaWm47Q9wgtG4\nBejcuqU/o9wTt83MxMsvt359XUmJWLVKeHk12jP69RPLl4uff37kuz6U3MVhSsdKXFyc7kvF\n09MzLCzs2WefjYyMHDNmTL9+/XTTY2NjtZ2wM3ViQJeXi0OHxJIlwt+/aXCqVMLFRbz7rkhJ\nERERbV2eLER1tbhw/Pb+xKtvvy2mTRMf9fqwCM7jcajFRHZ2FuPGicWLxdat4tSpVq8U7lQN\n62nPnNKUZKxPkCWgDR/V8NO0WrFunf7JhYCwsxPvvFP/mPWmamtFaKgA6s9F617u7mLuXLFv\nX9Mn8z4qGNBGk56eHh0d7ezsbPgNQK1Wu7m5RUdHH+20Z7IZOaALCsRXX4nly0VYmP6Bcg1f\nAweKlStFQIDw8RGAGD68xQ9ITRXbtonXXxeRkcLXV3Q31+TCow5m/rgIiP9higCW40NAWFmJ\nxx8Xc+boP77h4HQGEjdpG66uyaqbB7dkAd0a2Qt4+DJycvQDDupetratn1P99lsREyOOHRPr\n14tRo5omtZmZGDJELFokPv9cXLnyEFujLEoOaFMdD7q0tLSsrMzCwsLFxcWstSduGMmWLVvi\n4uIecDzoigpkZyMrC+fP49gxZGXh9u2m85ibY+RITJ6MyEj4+xsWrPjP7rx+o7Px2O+/4+pV\n/P47rlxBTg7u3Wv6AWrUXcBAT+QGm2Wq+vcL8ykYb3PC8rmIgKHdH3vsPmMCSz8IsmRrfIAV\nSbNIw2Xbs6BR/scOH8abb+KXX+qnPPEEpk/HM8/8eWojNRXjx+P557Fzp36O/HwkJ+N//8PR\no6ioaPqJPXti6FAMGoTAQAQGws8PDg4PVaJMlDwetKkGtJTaG9C//YbffkN+PvLy6gM1L6/l\nmc3Nq4KG3x4+4Y+gpwq9nrx1z7qoCDdvoqAAN27g5k3k5rYQxE1YWkKjwd/+Bn9/BPlWD+xX\n+diTDt27P+Bmtu0hY+iBl23PRzWPORO6PKOdAd3+zWl75oMHsXYtjhxpNI+nJ8aOxWyLPeM/\nia4bGaY++UPTxaqrceIEUlJw7Bh+/hlVVS1/urMzfHzg7Q1vb3h6wtMTbm5wc4OLCyws2rsB\nkmNAm7Z2BfTgwZpzWT8iRAPLEjjWwrwMtvfQowLW99CjFA7lqh5LzP7PTlU22/mb3Lo+xeVW\nzVskbejWDd7e6N8fAwbAxwe+vvD1hbc3LCyMlkRtx6gSnjbykGuXfRMMmldixG+U9nzU5cvY\ntQt79yIrq36iGbQjkHYRAbaeDgMGwLdPeVT+v+8OCqsJC+/VCw4OsLODvT26m9dYX0rHr7/i\n559x9iwyM3Xju96HoyN69YKTk/7yTDs72NnBwQG2trCxgbU17Oxgbg4HB5iZwd4eAOzsoFZD\npershjkDWgqlpaXh4eEA0tPTO7RgXl6eRqNpY4bdu3e/9dZbbQV0RUWNvbNFbeUw/HoaQzu0\n9oasrNC7Nzw84OYGd3esWwcAJ0/CywtubvXDAZvET8y4fQXG3XDZ29dGafIbZSuys/HNN0hJ\nwYkTTR/wG4PPP8PMXHj2xfXmC9rYwNLyz/CsqYFGY1arsVfdRXU1NBpoNG0X1wP3LFDT4XLN\nzBpdXNla513j1np3i9qE7b38pvi2PDMDWhq3b9/WnTzs0BZdvnzZx8enPXOWl5dbW1u39u7e\npWk7/337ACKav9WtG3r0gJ0dHB1hbw8HBzg4wNERTk5wckKvXnB2Rq9e6N3bRHvwjKnzotMQ\n8Ur4klPmbwPXruH0aVy4gEuXcOUKKi/nxxe++LWIWIdXjLkaOfwz5Fj8qbGtvcuAlkJNTU1q\naiqAv/zlLx1aMD8/v6q1PjUAwOnTp//+979XV1dbWlq2No8QOHUKFRXo0QMWFnBwgJUVbGz0\nv6URmSKtFrdu4Y8/8McfKC1FaSnKy3HvHsrLodGgqgqVlQDq/2LQfErL6uqg1aK2FrW1EKL+\nT0D/p1YL3QOdtVpotfVlNXnKc11dG19WPSw1Cbt6+4x1b20GJQe0ydxJeF8WFhYdjWadPn36\ntD1DQZOHWLdEpYLyfrhED8XMDL17t32D6kNSA2pAuecPZWeqAX337t2ysjIzMzNXV9fOvsyO\niEgWJhZtGRkZL7zwgpubm729vYeHR58+fSwtLT08PGJiYk6cOCF3dURExmRKLehFixZt3LhR\nCKEbsN/JyQlAcXFxXl7e7t27d+/ePXfu3I874QHGuq5nKysro38yESlEG2eYZGQyAb1p06bE\nxMQJEyZ8+OGHjz/+eJN3MzMz33vvvW3btgUEBCxZssS4qx4+fPiZM2dqdWctWhcWFrZgwYIh\nhiFAJVdQULBs2bL169c7OjrKVcOPP/64a9cueQd9/eKLL65du7Zs2TIZa0hISPDy8nr++edl\nrGHBggWzZ88OCQmRq4CSkpLFixcnJCT07sxu7LadOXNm48aNx48fb3s2c3PzwYMHS1NSx8h3\nl3nHyDhgfzvZ2Njs379frrULIS5dugTgxgMPRmcMe/bscXV1lbEAIcTy5csnTpwobw0TJ05c\n/mAP9zIeV1fXPXv2yFjAjRs3AFy6dEnGGvbv329jYyNjAQ/JZPqgMzIyQkJC7jtgf0ZGhpRV\nERF1HpMJaMOA/W3M84gM2E9EBMCEAnrmzJlZWVnPPPPM+fPnm7+bnZ09c+bMlJSUyMhI6Wsj\nIuoMJnOScP78+efPn9+8efM333zj6enp5eXVs2dPlUpVUlKSm5t79epVALGxsa+99prclRIR\nGYfJBDSApKSkefPmrV69+siRI4bTsmq12sXFJTo6et68eWPHtnq7PRGRyTGlgAYwZMiQzz//\nHNIO2E9EJAsTC2gDBwcHBw7+RkSPNLY9iYgUigFNRKRQDGijsbS0lPd2fktLS5VKJXsNso9p\nwBoUUgN3yIf36AzYL7vff/+9b9++8p6xvHLlSv/+/WUsoLa29saNG15eXjLWcO/evYqKChcX\nFxlruHXrlrW19YM8Bt54rl275u7u3sbNtxKQfYfUarXXr1/39vaWsYaHwYAmIlIodnEQESkU\nA5qISKEY0ERECsWAJiJSKAY0EZFCMaCJiBSKAU1EpFAMaCIihWJAExEpFAOaiEihGNBERArF\ngCYiUigGNBGRQjGgiYgUigFNnSUnJycxMVHuKuTRlbddge7du7djx468vDy5C+kwBrQxXb16\nNSYmxtfX18bGJjg4+PXXX79z546UBVRXV7/55ptjxoyxt7cfMGBATEzM5cuXpSygoQ0bNqxc\nuVLilSYlJYWFhTk4OISFhSUlJUm8dgNZtl1HCfuA7AdCE4sWLYqNjT179qyMNTwgQUby22+/\n2djYmJubjxs3Li4ubsSIEQACAwMrKyulKaC0tHT06NEABg4cOHfu3PHjx6tUqu7du6enp0tT\nQEOHDx+2srJycHCQcqVxcXEA/Pz85syZ89hjjwFYuHChlAXoyLLtOkrYB2Q/EJrYt2+fLuv2\n798vSwEPgwFtNNOmTVOpVMnJyYYpr776KoANGzZIU8CKFSsALFiwwDDl66+/NjMzGzx4sDQF\n6MycOdPPz093SEgZUunp6QAmTpxYU1MjhKipqdHF0/nz5yWrQa5tN1DCPiD7gdBQXl5ez549\ndc8eY0B3aa6ursOGDWs45dy5cwBefPFFaQrw9/e3tbWtqqpqOPGvf/0rgMLCQmlqEEJMnTp1\nypQpU6ZMsbW1lTKkoqOjAZw9e9Yw5ddffwUwZ84cyWqQa9sNlLAPyH4gGGi12nHjxvXr1++N\nN94w0YCW84GSjxKtVrty5comD0stLCwE4OPjI00NZmZmY8eOtbKyajhR90jjkpISyR6i+t//\n/lf3l+DgYClPyxw5csTDw2PQoEGGKUOHDnVzczt8+LBkNci17Qay7wNKOBAMPvroo6NHjx47\nduzEiRMSr9po5P6GeARVVFTcuHHjwIEDvr6+rq6u2dnZclVy69atbt26ubq66n7rl1hQUJBk\nrciSkhIAo0aNajJd1wF69+5dacowkHLb2ybjPiDvgZCenm5pablixQohRHx8PNiCJp0lS5Zs\n3rwZgI2NTWpqqq+vryxlZGdnT548uaqqKikpydz8Ef9Bl5WVAXBycmoyXTfl7t27tra2MpQl\nN3n3ARkPhMrKypkzZw4cOPCdd96RbKWd4RE/bjtDRUXFxx9/bPinj4/P5MmTG84QFxcXHh6e\nk5OzZcuW0NDQvXv3RkZGSllAeXn56tWrExIShBCJiYmxsbFGXHs7a5CYhYUFAJVK1eK7ZmZd\n7nJSCfaB++rsA6ENy5Ytu3Llyi+//KLr3jFhcjfhTU9BQUHD/8Dp06e3NueNGzdsbW3d3d2l\nLODAgQN9+/YFMGXKlKysLOOuup016Ej5a35dXZ1arR4zZkyT6SEhIWq1uq6uTpoyDOTt4pBm\nH2i/TjoQWvPtt98CWLt2rWGK6XZxMKCNIycnZ/Pmzc2v6AoPDwdQXFwsTRlvv/02gMDAwGPH\njkmzxjZIHFJubm79+/dvMtHT01OyXGhIxoCWdx9QwoGwZs2aNpqk27Ztk6AGY2EXh3EUFhbG\nxcUtXrx43bp1DacXFRX16NHD3t5eghp27Njx7rvvRkVF7dixw+SB0MK0AAAEH0lEQVR/s+u4\np556avfu3dnZ2bpbVABkZmbm5ubqLr/rImTfB5RwIAwePFh3y5JBenp6WlrapEmTvLy8/P39\nJajBaOT+hnhEaDQaFxcXe3v7y5cvGybu2bMHQGRkpAQFaLVaPz8/d3d3ue7Xak7iVuTRo0cB\nzJo1S/dPrVY7Y8YMAD/88INkNRjI0oJWwj4g+4HQItPt4mAL2jgsLCw2bNgQFRUVHBwcERHh\n4uJy8eLFlJQUV1fXjRs3SlDAtWvXLl261KtXr6lTpzZ/d9euXc7OzhKUIaOxY8fGxsZu3749\nPz8/JCTk+PHjqampL730UlhYmNylSUQJ+4DsB8KjRu5viEfK999/P3HiRCcnJ2tr68GDBy9Z\nskSy3ufvvvuujZ9yXl6eNGU0JH0rUqvVrlq1KjQ01M7OLjQ0VHcNgyxkaUErZx+Q8UBokem2\noFVCCCNHPhERGUOXuz6UiMhUMKCJiBSKAU1EpFAMaCIihWJAExEpFAOaiEihGNBERArFgCYi\nUigGNBGRQjGgiYgUigFNRKRQDGgiIoViQBMRKRQDmohIoRjQREQKxYAmIlIoBjQRkUIxoImI\nFIoBTUSkUAxoIiKFYkATESkUA5qISKEY0ERECsWAJiJSKAY0EZFCMaCJiBSKAU1EpFAMaCIi\nhWJAExEpFAOaiEihGNBERArFgCYiUigGNBGRQjGgiYgUigFNRKRQDGgiIoViQBMBQGZmppWV\nVXh4uGFKTU1NcHCwk5NTQUGBjIVRV8aAJgKAwMDAN9544+jRo5988oluSkJCQkZGxvr163v3\n7i1vbdRlqYQQctdApAgajWbYsGH5+flZWVl37twJDg5++umnk5OT5a6Lui4GNFG9tLS00NDQ\nqKiogoKC9PT0zMxMNzc3uYuirstc7gKIFGTEiBGvvPLK2rVrAezcuZPpTPJiC5qokZycHF9f\nXxsbm/z8fDs7O7nLoS6NJwmJGlm6dKmlpWV5efmKFSvkroW6OgY0Ub3PPvssOTk5Pj5++vTp\nSUlJJ0+elLsi6tLYxUGkV1hYGBgY6O3tnZaWVlhYGBAQ4OHhkZ6ebmlpKXdp1EWxBU2kN3/+\n/NLS0q1bt6rV6j59+nzwwQcXLlyIj4+Xuy7qutiCJgKAvXv3RkVFLV26dM2aNbopWq125MiR\nZ8+eTU9PDwgIkLc86poY0ERECsUuDiIihWJAExEpFAOaiEihGNBERArFgCYiUigGNBGRQjGg\niYgUigFNRKRQDGgiIoViQBMRKRQDmohIoRjQREQKxYAmIlIoBjQRkUIxoImIFIoBTUSkUAxo\nIiKFYkATESkUA5qISKEY0ERECsWAJiJSKAY0EZFCMaCJiBSKAU1EpFAMaCIihWJAExEpFAOa\niEihGNBERArFgCYiUigGNBGRQv0/eeEBnT/A1z4AAAAASUVORK5CYII=",
      "text/plain": [
       "Plot with title “Scaled Normal: Red, Mixture: Blue”"
      ]
     },
     "metadata": {
      "image/png": {
       "height": 450,
       "width": 600
      }
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "n<-500\n",
    "xp<-rnorm(n)\n",
    "yp<-M*dnorm(xp)*runif(n)\n",
    "\n",
    "plot(xgrid, Mnm, lwd=2, type=\"l\",col='red',main='Scaled Normal: Red, Mixture: Blue',xlab = 'x', ylab = 'y')\n",
    "lines(xgrid, mix, lwd=2, col='blue')\n",
    "\n",
    "dmix = w*dnorm(xp, mu1, sigma1) + (1-w)*dnorm(xp, mu2, sigma2)\n",
    "points(xp[yp>=dmix],yp[yp>=dmix], col='red',pch=20, cex=0.2)\n",
    "points(xp[yp<dmix],yp[yp<dmix], pch=16, cex=0.2, col='blue')"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "dbcdcd9c",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "#### Reject and accept method: the proof\n",
    "\n",
    "$$\\begin{aligned}\n",
    "                  P(V\\leq y |stopping~rule)&= P(V\\leq y | U < \\frac{1}{M} \\frac{f_Y(V)}{f_V(V)})\\\\\n",
    "                                           &= \\frac{P(V\\leq y , U < \\frac{1}{M} \\frac{f_Y(V)}{f_V(V)})}{P(U <\n",
    "                                             \\frac{1}{M} \\frac{f_Y(V)}{f_V(V)})}\\\\\n",
    "                                           &= \\frac{\\int_{-\\infty}^y\\int_0^{\\frac{1}{M}\n",
    "                                             \\frac{f_Y(V)}{f_V(V)}}du~f_V(v)dv}{\\int_{-\\infty}^{\\infty}\\int_0^{\\frac{1}{M}\n",
    "                                             \\frac{f_Y(V)}{f_V(V)}}du~f_V(v)dv}\\\\\n",
    "                                           &= \\frac{\\int_{-\\infty}^y\\frac{1}{M}\n",
    "                                             \\frac{f_Y(V)}{f_V(V)}f_V(V)dv}{\\int_{-\\infty}^{\\infty}\\frac{1}{M}\n",
    "                                             \\frac{f_Y(V)}{f_V(V)}f_V(V)dv}\\\\\n",
    "                                           &=\\int_{-\\infty}^y f_Y(v)dv\n",
    "                \\end{aligned}$$\n",
    "\n",
    "-   Can have any $M$? In fact $M$ shows the efficiency of the sampling\n",
    "    algorithm, i.e. $M= 1/P(stopping~rule)$.\n"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "fc6bd2ac",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "#### Choosing $f_v(x)$ and $M$\n",
    "\n",
    "-   Two things are necessary for the accept/reject algorithm to work:\n",
    "\n",
    "    1.  The domain of $p(x)$ and the domain of $q(x)$ MUST be the same.\n",
    "\n",
    "    2.  The value of $M$ must satisfy $M\\geq \\sup_x p(x)/q(x)$\n",
    "\n",
    "-   The algorithm will be more **efficient** if:\n",
    "\n",
    "    1.  The proposal $q(x)$ is a good approximation to $p(x)$\n",
    "\n",
    "    2.  The value of $M$ is $M=\\sup_x p(x)/q(x)$"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "07d906e3",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "#### A look at $f_y(x)/f_v(x)$\n",
    "\n",
    "\n",
    "\n",
    "Normalizing Constant and Kernel\n",
    "\n",
    "-   Today we saw many density functions $f(x)$\n",
    "\n",
    "-   Many density functions can written as $f(x)=k\\tilde{f}(x)$\n",
    "\n",
    "-   The part $k$ is called the normalizing constant and the part\n",
    "    $\\tilde{f}(x)$ is called the kernel.\n",
    "\n",
    "-   For example the standard normal distribution is\n",
    "    $$p(x)=(2\\pi)^{-1/2}e^{-x^2/2}$$\n",
    "\n",
    "Normalizing Constant and Kernel What are the normalizing constant and\n",
    "kernel of the Beta function?\n",
    "\n",
    "$$Beta(x;a,b)=\\frac{\\Gamma(a+b)}{(\\Gamma(a)\\Gamma(b))}{x^{a-1}(1-x)^{b-1}}$$"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "1af07f3b",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "### Accept/Reject and the normalising constant\n",
    "\n",
    "-   An advantage of the Accept/Reject algorithm is that is works, even\n",
    "    if the normalizing constant is unavailable.\n",
    "\n",
    "-   Only the kernel is needed.\n",
    "\n",
    "-   There are many examples where the normalising constant is either\n",
    "    unavailable or difficult to compute.\n",
    "\n",
    "-   This often happens in Bayesian analysis\n"
   ]
  }
 ],
 "metadata": {
  "celltoolbar": "Slideshow",
  "kernelspec": {
   "display_name": "R",
   "language": "R",
   "name": "ir"
  },
  "language_info": {
   "codemirror_mode": "r",
   "file_extension": ".r",
   "mimetype": "text/x-r-source",
   "name": "R",
   "pygments_lexer": "r",
   "version": "4.3.2"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 5
}